# 聊聊前缀树 Trie

# Trie 树简介

Trie 树，也叫“字典树”。顾名思义，它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。

此外 Trie 树也称前缀树（因为某节点的后代存在共同的前缀，比如 pan 是 panda 的前缀）。

它的 key 都为字符串，能做到高效查询和插入，时间复杂度为 O(k)，k 为字符串长度，缺点是如果大量字符串没有共同前缀时很耗内存。

它的核心思想就是通过最大限度地减少无谓的字符串比较，使得查询高效率，即「用空间换时间」，再利用共同前缀来提高查询效率。

# Trie 树特点

假设有 5 个字符串，它们分别是：code，cook，five，file，fat。现在需要在里面多次查找某个字符串是否存在。常见的方案有：①如果每次查找，都是拿要查找的字符串跟这 5 个字符串依次进行字符串匹配，时间复杂度为 O(n)。②将字符串存入 HashSet 中，查找的时候时间复杂度为 O(1)，但是缺点是空间复杂度高，假如有大量的字符串（比如 10 亿条）则会浪费大量的空间。

Trie 树则通过空间换时间的方式，将字符串组织成下图的结构：

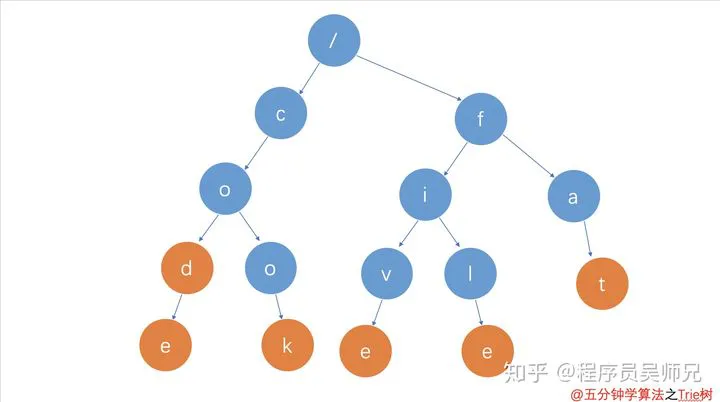
v2-d82b7d102ad949dce0bfb92af3d41a11_720w

通过上图，可以发现 Trie 树的三个特点：

根节点不包含字符，除根节点外每一个节点都只包含一个字符
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
每个节点的所有子节点包含的字符都不相同

# Trie 树的插入操作

Trie 树的插入操作很简单，其实就是将单词的每个字母逐一插入 Trie 树。插入前先看字母对应的节点是否存在，存在则共享该节点，不存在则创建对应的节点。比如要插入新单词cook，就有下面几步：

插入第一个字母 c，发现 root 节点下方存在子节点 c，则共享节点 c
插入第二个字母 o，发现 c 节点下方存在子节点 o，则共享节点 o
插入第三个字母 o，发现 o 节点下方不存在子节点 o，则创建子节点 o
插入第三个字母 k，发现 o 节点下方不存在子节点 k，则创建子节点 k
至此，单词 cook 中所有字母已被插入 Trie 树中，然后设置节点 k 中的标志位，标记路径 root->c->o->o->k 这条路径上所有节点的字符可以组成一个单词cook

# Trie 树的查询操作

在 Trie 树中查找一个字符串的时候，比如查找字符串 code，可以将要查找的字符串分割成单个的字符 c，o，d，e，然后从 Trie 树的根节点开始匹配。如图所示，绿色的路径就是在 Trie 树中匹配的路径

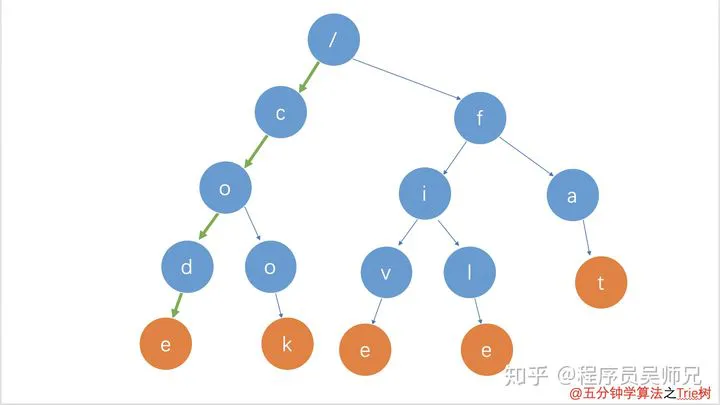
# Trie 树的删除操作

Trie 树的删除操作与二叉树的删除操作有类似的地方，需要考虑删除的节点所处的位置，这里分三种情况进行分析： 删除整个单词（比如hi）

从根节点开始查找第一个字符h
找到h 子节点后，继续查找h 的下一个子节点i
i 是单词hi 的标志位，将该标志位去掉
i 节点是hi 的叶子节点，将其删除
删除后发现h 节点为叶子节点，并且不是单词标志位，也将其删除
这样就完成了hi 单词的删除操作

删除前缀单词（比如cod）

这种方式删除比较简单。只需要将cod 单词整个字符串查找完后，d 节点因为不是叶子节点，只需将其单词标志去掉即可。

删除分支单词（比如cook）

与 删除整个单词 情况类似，区别点在于删除到 cook 的第一个 o 时，该节点为非叶子节点，停止删除，这样就完成cook 字符串的删除操作。

# Trie 树应用与实现

事实上 Trie 树在日常生活中的使用随处可见，比如这个：具体来说就是经常用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

实现：最简单的字典树

class TrieNode {
    String word;
    boolean isEnd;
    TrieNode[] children;
    public TrieNode() {
        children = new TrieNode[26];
    }
}

# 前缀匹配/自动补全

例如：找出一个字符串集合中所有以 五分钟 开头的字符串。我们只需要用所有字符串构造一个 trie 树，然后输出以五−>分−>钟开头的路径上的关键字即可。 trie 树前缀匹配常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能

实现：自动补全功能

（1）先找出匹配词语的节点（可能是中间的路径，不一定是最终节点）

（2）递归的查询该节点下的所有单词

public class Trie {
    private class TrieNode {
        String word;
        boolean isEnd;
        Map<Character, TrieNode> children;
        public TrieNode() {
            children = new HashMap<>();
        }
    }
    TrieNode root;
    public Trie() {
        root = new TrieNode();
    }
    public void insert(String word) {
        TrieNode node = root;
        for (char c : word.toCharArray()) {
            if (!node.children.containsKey(c)) {
                node.children.put(c, new TrieNode());
            }
            node = node.children.get(c);
        }
        node.isEnd = true;
        node.word = word;
    }
    public List<String> autoComplete(TrieNode node, String word) {
        List<String> res = new ArrayList<>();
        for (char c : word.toCharArray()) {
            if (!node.children.containsKey(c)) {
                node = node.children.get(c);
            }
        }
        helper(node, res);
        return res;
    }
    private void helper(TrieNode node, List<String> words) {
        if (node.isEnd) {
            words.add(node.word);
        }
        for (Map.Entry<Character, TrieNode> entry : node.children.entrySet()) {
            helper(entry.getValue(), words);
        }
    }
}

# 字符串检索

给出 N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，按最早出现的顺序写出所有不在熟词表中的生词。检索/查询功能是 Trie 树最原始的功能。给定一组字符串，查找某个字符串是否出现过，思路就是从根节点开始一个一个字符进行比较：

如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。
如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

public class Trie {
    private class TrieNode {
        String word;
        boolean isEnd;
        Map<Character, TrieNode> children;
        public TrieNode() {
            children = new HashMap<>();
        }
    }
    TrieNode root;
    public Trie() {
        root = new TrieNode();
    }
    public void insert(String word) {
        TrieNode node = root;
        for (char c : word.toCharArray()) {
            if (!node.children.containsKey(c)) {
                node.children.put(c, new TrieNode());
            }
            node = node.children.get(c);
        }
        node.isEnd = true;
        node.word = word;
    }
    public boolean search(String word) {
        TrieNode node = root;
        for (char c : word.toCharArray()) {
            if (!node.children.containsKey(c)) {
                return false;
            }
            node = node.children.get(c);
        }
        return node.isEnd;
    }
}

# 动态路由

实现动态路由最常用的数据结构，被称为前缀树(Trie 树)。看到名字你大概也能知道前缀树长啥样了：每一个节点的所有的子节点都拥有相同的前缀。这种结构非常适用于路由匹配，比如我们定义了如下路由规则：

/:lang/doc
/:lang/tutorial
/:lang/intro
/about
/p/blog
/p/related

HTTP 请求的路径恰好是由/分隔的多段构成的，因此，每一段可以作为前缀树的一个节点。我们通过树结构查询，如果中间某一层的节点都不满足条件，那么就说明没有匹配到的路由，查询结束。

接下来我们实现的动态路由具备以下两个功能。

参数匹配:。例如 /p/:lang/doc，可以匹配 /p/c/doc 和 /p/go/doc。
通配*。例如 /static/*filepath，可以匹配/static/fav.ico，也可以匹配/static/js/jQuery.js，这种模式常用于静态服务器，能够递归地匹配子路径。

实现：动态路由

（1）由于路由规则允许模糊匹配，匹配子节点时可能还包括了含有模糊字符串的结构，比如插入/:lang/tutorial 这个路由 pattern 后再插入/golang/intro 时，虽然 golang 与:lang 并不匹配，但还是需要将 intro 插入在:lang 节点下，而不是再创建一个 golang 节点，所以仅使用哈希表查找子节点并不合适，需要改用为 ArrayList 来存 TrieNode，使用一个单独的字符串 part 来保存节点的信息，isWild 来判断节点是否是模糊节点。

（2）插入与查询的逻辑与字符串检索区别不大，关键修改在于：插入时还需要插入 part 和 isWild 信息，搜搜时如果碰到了*号开头的节点，需要终止查询，返回该节点。

public class Trie {
    private class TrieNode {
        String part;
        String pattern;
        boolean isWild;
        boolean isEnd;
        List<TrieNode> children;
        public TrieNode() {
            children = new ArrayList<>();
        }
        public TrieNode(boolean isWild, String part) {
            this.isWild = isWild;
            this.part = part;
            children = new ArrayList<>();
        }
    }
    private TrieNode root;
    public Trie() {
        root = new TrieNode();
    }
    public List<String> parsePattern(String pattern) {
        String[] parts = pattern.split("/");
        List<String> res = new ArrayList<>();
        for (String part : parts) {
            if (part.isEmpty()) {
                continue;
            }
            res.add(part);
            if (part.charAt(0) == '*') {
                break;
            }
        }
        return res;
    }
    public TrieNode matchChild(TrieNode node, String part) {
        for (TrieNode child : node.children) {
            if ((child.part != null && child.part.equals(part)) || child.isWild) {
                return child;
            }
        }
        return null;
    }
    public List<TrieNode> matchChildren(TrieNode node, String part) {
        List<TrieNode> children = new ArrayList<>();
        for (TrieNode child : node.children) {
            if ((child.part != null && child.part.equals(part)) || child.isWild) {
                children.add(child);
            }
        }
        return children;
    }
    public void insert(String pattern) {
        List<String> parts = parsePattern(pattern);
        insert(root, pattern, parts, 0);
    }
    private void insert(TrieNode node, String pattern, List<String> parts, int depth) {
        if (parts.size() == depth) {
            node.pattern = pattern;
            node.isEnd = true;
            return;
        }
        String part = parts.get(depth);
        TrieNode child = matchChild(node, part);
        if (child == null) {
            boolean isWild = part.charAt(0) == ':' || part.charAt(0) == '*';
            child = new TrieNode(isWild, part);
            node.children.add(child);
        }
        insert(child, pattern, parts, depth + 1);
    }
    public TrieNode search(TrieNode node, int depth, List<String> parts) {
        if ((parts.size() == depth) || (node.part != null && node.part.startsWith("*"))) {
            if (node.isEnd) {
                return node;
            }
            return null;
        }
        String part = parts.get(depth);
        List<TrieNode> children = matchChildren(node, part);
        for (TrieNode child : children) {
            TrieNode result = search(child, depth + 1, parts);
            if (result != null) {
                return result;
            }
        }
        return null;
    }
    public String getPattern(String path) {
        List<String> searchParts = parsePattern(path);
        TrieNode node = search(root, 0, searchParts);

        if (node != null) {
            return node.pattern;
        }
        return null;
    }
}

# Trie 树的局限性

如前文所讲，Trie 的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。假设字符的种数有m 个，有若干个长度为 n 的字符串构成了一个 Trie 树，则每个节点的出度为 m（即每个节点的可能子节点数量为m），Trie 树的高度为n。很明显我们浪费了大量的空间来存储字符，此时 Trie 树的最坏空间复杂度为O(m^n)。也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时 Trie 树的最坏时间复杂度为O(n)。这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。