# SSE 与 AVE 向量化编程
# 一、 向量化编程简介
近年来，CPU 已经达到了一些物理和功率限制，因此在 GHz 方面，CPU 速度并没有显著提高。随着计算需求的不断增加，CPU 设计人员决定用三种解决方案来解决这个问题：
- 增加更多核心。通过这种方式，操作系统可以在不同的内核之间分配正在运行的应用程序。此外，程序还可以创建多个线程来最大化核心使用率
- 将向量化操作应用到每个核心。该解决方案允许 CPU 对数据向量执行相同的指令。这只能在应用程序级别完成
- 多条指令的无序执行。如果现代 CPU 是独立的，那么它们最多可以同时执行四条指令。
向量寄存器始于 1997 年的 MMX 指令集。MMX 指令集具有 80 位的寄存器。之后发布了 SSE 指令集（从 SSE1 到 SEE4.2 有多个版本），具有 128 位寄存器。2011 年，英特尔发布了采用 AVX 指令集（256 位寄存器）的 Sandy Bridge 架构。2016 年，首款 AVX-512 CPU 发布，采用 512 位寄存器（最多 16x 32 位浮点矢量）。
本文将重点介绍 SSE 和 AVX 指令集，因为它们通常出现在最近的处理器中。AVX-512 不在讨论范围内，但只需将 256 位寄存器更改为 512 位对应寄存器(ZMM 寄存器)，即可将本文中的所有示例应用于 AVX-512。
# 1. SSE/AVE 寄存器
SSE 和 AVX 各有 16 个寄存器。在 SSE 中，它们被称为 XMM0-XMM15，而在 AVX 中，它们被称为 YMM0-YMM15。XMM 寄存器长度为 128 位，而 YMM 为 256 位。
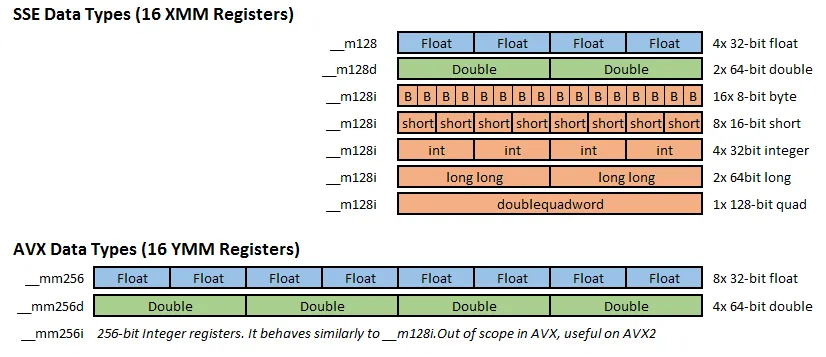
SSE 增加了三个类型定义： __m128 、 __m128d 和 __m128i 。分别为浮点型、双精度型(D)和整型(I)。
AVE 增加了三个类型定义： __m256 、 __m256d 和 __m256i 。分别为浮点型、双精度型(D)和整型(I)。
警告
XMM 和 YMM 是重叠的：XMM 寄存器被视为相应 YMM 寄存器的下半部分。这可能会在混合使用 SSE 和 AVX 代码时带来一些性能问题。
浮点数据类型（如__m128、__m128d、__m256 和__m256d）在 GCC 编译器中被视为具有相同数据结构的类型。因此，GCC 允许以数组的形式访问这些数据类型的组件。即：下面代码是合法的。
__m256 myvar = _mm256_set1_ps(6.665f); // Set all vector values to a single float
myvar[0] = 2.22f; // This is valid in GCC compiler
float f = (3.4f + myvar[0]) * myvar[7]; // This is valid in GCC compiler
例如，对于__m128 类型的变量，可以通过索引来访问其中的四个单精度浮点数组件。对于__m128d 类型的变量，可以通过索引来访问其中的两个双精度浮点数组件。类似地，对于__m256 和__m256d 类型的变量，可以通过索引来访问其中的八个单精度浮点数或四个双精度浮点数组件。
而在 GCC 编译器中，__m128i 和__m256i 是用于处理整数向量的数据类型。它们被定义为联合体（union），可以表示不同长度的整数向量。然而，由于联合体的特性，访问其中的具体数据成员可能会有一些困难。为了从整数向量中提取单个数据值，可以使用 _mm_extract_epiXX() 函数。这些函数允许从整数向量中提取指定位置的数据值，并将其作为标量返回。 _mm_extract_epiXX() 函数中的 XX 表示整数向量的位宽，例如， _mm_extract_epi32() 用于从 32 位整数向量中提取单个 32 位整数值。
# 2. AVE 操作例子
执行 AVX 指令的过程如下：
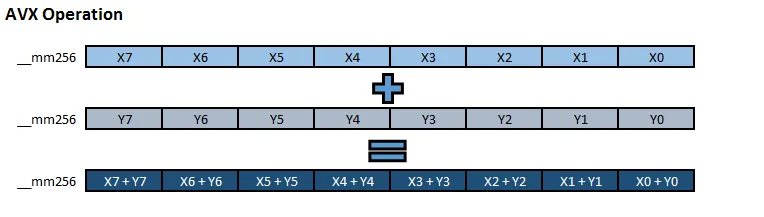
所有操作同时进行。就性能而言，在 AVX 中对浮点数执行单个 Add 的消耗与在 AVX 中对 8 个浮点数执行 VAdd 的消耗近似。在Agner Fog’s instruction tables
中，可以获得更多有关指令延迟和吞吐量的信息。在 Sandy Bridge 架构上，VADDPS/D 的延迟为 3，吞吐量为 1，就像 FADD(P) 一样。
# 3. 先决条件
SSE/AVX 需要目标机器具备相应的硬件支持。因此，为了确保程序在目标机器上能够正常运行，需要满足这些指令集扩展的先决条件。本文中的示例代码为了简化构建过程并确保程序在当前机器上正常运行，使用-march=native 编译选项。这个选项会自动检测当前机器的 CPU 能力，并使用相应的指令集扩展。这样可以充分利用目标机器的硬件能力，提高程序的性能和效率。
警告
注意：编译后的二进制文件在没有 AVX 功能的计算机上将失败。如果需要适应不同 CPU 的二进制代码，则需要利用 CPU Flag 并调用不同的函数，或者针对不同的指令集生成不同的二进制代码。
由于操作系统、编译器和 CPU 都必须允许 SSE/AVX 扩展。我们可以运行以下脚本来检测系统功能：
#!/bin/bash
#CPU flag detection
echo -e "\e[32m>>> Getting CPU flag capabilities and number of cores\e[0m"
cat /proc/cpuinfo | egrep "(flags|model name|vendor)" | sort | uniq -c
#Compiler capabilities. -march=native is required!
echo -e "\e[32m>>> Getting GCC capabilities\e[0m"
gcc -march=native -dM -E - < /dev/null | egrep "SSE|AVX" | sort
#OS kernel version
echo -e "\e[32m>>> Getting OS Kernel Version\e[0m"
uname -a
在 CPU Flag 中，我们可以看到 SSE 和 AVX 的支持。我们将搜索 avx 标志。这表明 CPU 兼容 AVX。如果有 avx2，则表示 CPU 允许 AVX2 扩展。AVX 足以支持 8x32 位浮点矢量。AVX2 为整数增加了 256 位向量（例如 8x32 位整数）。尽管如此，256 位整数向量的执行速度似乎与两个 128 位向量相同，因此与 SSE 128 位整数向量相比，性能并没有显著提高。
在 GCC 的输出中，我们可以看到 #define __AVX__ 1 等。这表明 GCC 允许使用 AVX 指令集扩展。
重要
记住始终使用 -march=native 或 -mavx， 如果运行 GCC 时没有使用正确的 march，就不会得到 AVX 标志！ 默认的 GCC 参数是通用的，如果没有该标记，即使 CPU 支持 AVX，也无法启用 AVX。
最后，我们需要再次检查 Linux 内核是否为 2.6.30 或更高版本。理想的内核是 4.4.0 或更高版本。
有了所有这些先决条件，我们就可以开始编写第一个 AVX 向量程序了。
# 二、自动向量化
# 1. GCC 自动向量化 flag
GCC 是一种高级编译器，使用优化标志 -O3 或 -ftree-vectorize 时，编译器会搜索循环向量化（需要指定-mavx flag）。在源代码保持不变的情况下，GCC 编译出来的代码会完全不同。
除非启用某些标志，否则 GCC 不会记录任何有关自动向量化的内容。如果需要自动向量化结果的详细信息，可以使用以下编译器 flag
-fopt-info-vec或-fopt-info-vec-optimized：编译器将记录哪些循环（按行号）正在进行向量化优化。-fopt-info-vec-missed：关于未被向量化的循环的详细信息，以及许多其他详细信息。-fopt-info-vec-note：关于所有循环和正在进行的优化的详细信息。-fopt-info-vec-all：所有以上的选项放在一起。
注释
注意：还有类似的 -fopt-info-[options]-optimized 标志用于其他编译器优化，如内联： -fopt-info-inline-optimized
在以下示例中，我们将使用 -O3 和 -fopt-info-vec-optimized 启用 GCC 自动向量化。当然也可以更改编译器标志以查看不同的日志记录选项。
// autovector.cpp
// compile: g++ -fopt-info-vec-optimized -o autovector autovector.cpp
#pragma GCC optimize("O3", "unroll-loops", "omit-frame-pointer", "inline") // 优化选项
#pragma GCC option("arch=native", "tune=native", "no-zero-upper") // 启用 AVX
#pragma GCC target("avx") // 启用 AVX
#include <bits/stdc++.h>
#include <x86intrin.h> // AVX/SSE 指令集
int main()
{
const int N = 200000;
const int numTests = 10000;
float a[N], b[N], c[N], result[N];
auto start = std::chrono::high_resolution_clock::now();
// 数据初始化
for (int i = 0; i < N; ++i)
{
a[i] = ((float)i) + 0.1335f;
b[i] = 1.50f * ((float)i) + 0.9383f;
c[i] = 0.33f * ((float)i) + 0.1172f;
}
for (int i = 0; i < numTests; ++i)
{
for (int j = 0; j < N; ++j)
{
result[j] = a[j] + b[j] - c[j] + 3 * (float)i;
}
}
auto end = std::chrono::high_resolution_clock::now();
auto duration = std::chrono::duration_cast<std::chrono::microseconds>(end - start).count();
assert(result[2] == (2.0f + 0.1335f) + (1.50f * 2.0f + 0.9383f) - (0.33f * 2.0f + 0.1172f) +
3 * (float)(numTests - 1));
std::cout << "CG> message -channel \"results\" Time used: " << duration
<< "s, N * numTests=" << (N * numTests) << std::endl;
return 0;
}
如果一切正常，将看到编译器测试结果：
autovector.cpp:15:23: optimized: loop vectorized using 32 byte vectors
- 将编译选项更改为
-fopt-info-vec-all，可以看到更多的信息，包括向量化的循环的行号。 - 在 autovector.cpp 第 1 行，将 O3 改为 O2 , 然后重新运行。将不会看到 loop vectorized ，而且非向量化编译会比向量化编译慢。
# 2. 循环向量化的要求
并非所有循环都能进行向量化。要进行向量化，对循环有一些严格的要求。
- 一旦循环开始，循环计数就不能改变。这意味着，循环的终点可以是一个动态变量，可以随意增加或减少其值，但一旦循环开始，它就必须保持不变。
- 使用 break 或 continue 句子会有一些限制。有时编译器会很聪明地让它起作用，但在某些情况下，循环不会被向量化。
- 在循环内调用外部函数有一些限制
- 循环不应该有数据依赖关系。
- 条件句 (if/Else) 可以在不改变控制流的情况下使用，并且只用于有条件地将 A 或 B 值加载到 C 变量中。选择 A 或 B 是在编译器中使用掩码完成的，因此它同时计算分支 A 和 B ，而 C 将存储一个或另一个值：
if ( s >= 0 ) {
x[i] = (-b[i]+s)/(2.0f*a[i]);
y[i] = (-b[i]-s)/(2.0f*a[i]);
}
else {
x[i] = 0.0f;
y[i] = 0.0f;
}
这是一个可向量循环。控制流从未改变，x[i] 和 y[i] 值总是设置为其中一个或另一个值。
有关自动向量化的更多信息，请阅读Intel C++编译器的矢量化 。该文档虽然面向 Intel 编译器，但它提供了有关自动向量化的有趣而完整的信息。
自动向量化的好处是，它是自动完成的。编译器会尝试向量化循环，开发人员不需要做任何事情。但是有时(尤其是在高性能计算应用中)需要微调循环和向量化，通过使用手动 AVX 向量化来确保最大吞吐量。
# 三、SSE/AVX 的使用
支持 SSE/AVX 的 CPU 具有用于操作 XMM 和 YMM 寄存器的汇编指令。但在大多数编译器中，通过使用内置函数简化了这一过程，因此开发人员不需要直接使用汇编。
# 1. 内置函数
编译器将汇编指令封装为函数，使用它们就像调用带有正确参数的函数一样简单。有时，如果 CPU 不支持指令集，些内置函数就会被模拟。
SSE/AVX 内置函数使用以下命名约定：
_<vector_size>_<intrin_op>_<suffix>
<vector_size>是指向量的大小。对于 128 位的 SSE， 它为mm，对于 256 位的 AVX/AVX2，它为mm256，对于 512 位的 AVX512， 它为mm512。<intrin_op>是指内置函数的名称，例如add或sub，mul等 。<suffix>是指内置函数的参数类型，例如ps表示 float ，pd表示 double ，epi8表示 int8_t，epi32表示 int32_t ,epu16表示 uint16_t 等。
你可以在Intel Intrinsics Guide 中找到所有内置函数，它是 SSE/AVX 中提供的任何内置函数的完整参考。此外，还有一份 x86 内置函数 Cheet Sheet ，但由于内容更为复杂，阅读起来比较困难。
# 2. SSE/AVX 没有提供的内置函数
缺少整数除法：由于某些原因，SSE 和 AVX 缺少整数除法运算符。有一些方法可以克服这一点：
- 在线性代码中通过计算除法来完成操作。首先，从向量中取出单个数据，然后进行除法运算，最后将结果再次存储回向量中。然而，这种方法速度较慢。
- 将整数向量转换为浮点数，将它们相除，然后再次转换为整数。
- 对于编译时的已知除数，有一些魔法数（magic number）可以将常量除法转换为乘法运算。可以参考libdivide 。
- 对于 2 的幂除法，使用位移操作。除以整数 2 等于右移。只有当所有向量都被相同的 2 的幂整除时，才能进行右移操作。不过对有符号数进行右移时要注意！需要使用符号位移。
缺少三角函数：内置函数中没有三角函数。可能的解决办法是用线性代码计算（对每个向量值逐一计算），或创建近似函数。泰勒级数和 Remez 近似函数的效果很好。
缺少随机数生成器：此外，没有随机数生成器。但是从线性版本重新创建一个好的伪随机生成器是很简单的。只需确定伪随机数生成器中使用的位即可。填充向量首选 32 位或 64 位 RNG。
# 3. 性能损失
数据对齐： 旧的 CPU 架构不能使用向量化，除非数据在内存中与向量大小一致。其他一些 CPU 可以使用未对齐的数据，但性能会有所损失。在最近的处理器中，这种影响似乎可以忽略不计。但为了安全起见，如果不增加过多的开销，对齐数据可能是个好主意。有关数据对齐的资料，可参考Data alignment for speed: myth or reality?
- 在 GCC 中，可以使用以下变量属性进行数据对齐：
__attribute__((aligned(16)))、__attribute__((aligned(32))) - 最简单的变量对齐声明：
#define ALIGN __attribute__((aligned(32)))
- 在 GCC 中，可以使用以下变量属性进行数据对齐：
SSE/AVX 转换损失： 将传统的 SSE 库与新的 AVX 架构混合使用还有一个大问题。由于 XMM 和 YMM 共享低 128 位，在 AVX 和 SSE 之间转换可能导致高 128 位出现未定义的值。为了解决这个问题，编译器需要保存高 128 位，清除它，执行旧的 SSE 操作，然后恢复旧值。但是这显著增加了 AVX 操作的开销，导致性能下降。
警告
注意：这个问题并不意味着不能同时使用__m128 和__m256 而不影响性能。AVX 有一个针对__m128 的新指令集，带有 VEX 前缀。这些新的 VEX 指令与__M256 指令相结合没有任何问题。当非 VEX __m128 指令与 __m256 指令结合使用时，就会产生转换代价。当使用旧的 SSE 库链接到新的启用 AVX 的程序时，就会发生这种情况。
为了避免转换损失，编译器可以使用
-mvzeroupper参数自动添加对VZEROUPPER(清除高 128 位)或VZEROALL（清除所有 YMM 寄存器）的调用，程序员也可以手动添加。如果不使用外部 SSE 库，且确定所有代码都启用了 VEX 并在编译时启用了 AVX 扩展，则可以使用-mvzeroupper参数指示编译器避免添加VZEROUPPER调用：-mno-vzeroupper。更多关于 SSE/AVX 转换损失的资料，可参考Avoiding AVX-SSE Transition Penalties 和 Why is this SSE code 6 times slower without VZEROUPPER on Skylake? 。数据移动成本：在 AVX 寄存器中来回移动数据的成本很高。在某些情况下，如果有一些数据存储在线性结构中，那么将这些数据发送到 AVX 向量、执行一些操作并恢复这些数据的成本要比简单地执行线性计算高。因此，开发时必须考虑到数据加载和卸载的开销。请记住，在某些情况下，这将成为性能瓶颈。
# 4. AVX 使用例子：计算平方根
- 下面程序是对浮点数的 SQRT 计算进行向量化，显式使用
__m256数据类型来存储浮点数，从而减少数据加载的开销。
// vectorized_sqrt.cpp
// compile: g++ -o vectorized_sqrt vectorized_sqrt.cpp
#pragma GCC optimize("O3", "unroll-loops", "omit-frame-pointer", "inline") // 优化选项
#pragma GCC option("arch=native", "tune=native", "no-zero-upper") // 启用 AVX
#pragma GCC target("avx") // 启用 AVX
#include <bits/stdc++.h>
#include <x86intrin.h> // AVX/SSE 指令集
const int N = 64000000;
const int V = N / 8;
float linear[N];
// 禁用自动向量化
__attribute__((optimize("no-tree-vectorize"))) inline void normal_sqrt()
{
for (int i = 0; i < N; ++i)
{
linear[i] = sqrtf(linear[i]);
}
}
__m256 ALIGN vectorized[V];
inline void avx_sqrt()
{
for (int i = 0; i < V; ++i)
{
vectorized[i] = _mm256_sqrt_ps(vectorized[i]);
}
}
#define TIME \
std::chrono::duration_cast<std::chrono::duration<double>>( \
std::chrono::high_resolution_clock::now() - now) \
.count()
int main(int argc, char **argv)
{
// 数据初始化
for (int i = 0; i < N; ++i)
{
linear[i] = ((float)i) + 0.1335f;
}
for (int i = 0; i < V; ++i)
{
for (int v = 0; v < 8; ++v)
{
vectorized[i][v] = ((float)(i * 8 + v)) + 0.1335f;
}
}
// normal_sqrt benchmark
auto now = std::chrono::high_resolution_clock::now();
for (int i = 0; i < 20; ++i)
{
normal_sqrt();
}
auto linear_time = TIME;
std::cerr << "Normal sqrtf: " << linear_time << std::endl;
// AVX sqrt benchmark
now = std::chrono::high_resolution_clock::now();
for (int i = 0; i < 20; ++i)
{
avx_sqrt();
}
auto avx_time = TIME;
std::cerr << "AVX sqrtf: " << avx_time << std::endl;
// Check Values
for (int i = 0; i < V; ++i)
{
for (int v = 0; v < 8; ++v)
{
if (abs(linear[i * 8 + v] - vectorized[i][v]) > 0.00001f)
{
std::cerr << "Error: AVX sqrtf is not equal to normal sqrtf!" << std::endl;
std::cerr << "linear[" << i * 8 + v << "] = " << linear[i * 8 + v] << std::endl;
std::cerr << "vectorized[" << i << "][" << v << "] = " << vectorized[i][v]
<< std::endl;
return -1;
}
}
}
std::cout << "Linear to AVX improvement : " << (linear_time / avx_time * 100) << "%"
<< std::endl;
return 0;
}
- 可能会看到 600% 或更高的性能提升。也就是说，一旦加载了数据，AVX 的运行速度将是普通 sqrtf 的 7 倍。理论极限是 800%，但很少能达到。一般来说可以预期平均提高 300% 到 600%。运行结果如下：
Normal sqrtf: 1.51901
AVX sqrtf: 0.374871
Linear to AVX improvement : 405.209%
- 可以看到：运行速度提高了 405%。
# 四、C++中的 SSE/AVX 框架
# 1. 内置函数的复杂性
直接使用内置函数会使代码编写和维护变得复杂。问题在于内置函数名很长，比如算术运算用函数符号书写：add(a,b) 而不是 a + b。导致下面的代码很难阅读：
x = _mm256_div_ps(_mm256_add_ps(b, _mm256_sqrt_ps(_mm256_sub_ps(_mm256_mul_ps(b, b),
_mm256_mul_ps(_mm256_mul_ps(a, c),
_mm256_set1_ps(4.0f))))) , _mm256_mul_ps(a,_mm256_set1_ps(2.0f)));
而以下封装版本的可读性非常好：
x = (b + sqrt(b * b - a * c * 4.0f)) / (a * 2.0f);
# 2. 用于 SIMD 计算的 C++框架
现有的一些框架在新的类中封装了向量数据类型。然后，它们重载算术、逻辑和赋值运算符，以简化计算。其中，可以使用这两个框架：
- Agner Fog’s C++ vector class library ： 内容完整，定期更新。而且还包含了三角函数。
- Unified Multicore Environment ：一个较新的库
- xsimd Wrapper ：一个比较好用的 C++ Wrapper。
不过，这些库的体积都比较大，在代码大小有限（小于 100kb）的情况下，可以使用以下简单的封装版本，只需要关注一两种类型。
- 除了内置函数，该封装版本还封装了一些特殊的函数：
- Blend-based functions：blend 是根据掩码有条件地加载向量值的过程，这类函数用于混合两个向量的函数。
if_select(mask,value_true,value_false)：根据掩码对向量进行有条件加载。如果掩码为真，则返回 value_true，否则返回 value_false。if_add(mask,value,add_when_true)：条件加法。返回value + (mask? add_when_true:0)，对于每个向量分量。if_sub, if_mul, if_div：与 if_add 类似，只是算术运算方式不同。
- Horizontal functions：Horizontal 表示这些函数通过计算某些逻辑值或算术值，在单个向量变量内运行。
horizontal_or(mask)：如果掩码中的任何向量分量为 true。返回布尔值。horizontal_add(vector)：返回向量的所有分量的总和。返回值是一个数字(浮点型、双精度型或整型，具体取决于向量类型)。
# 五、Masking 与 Conditional Load
# 1. 向量中的掩码
掩码是向量之间逻辑运算的结果。它与布尔运算有许多相似之处（它们是对单个数字或其他布尔运算的逻辑运算结果），但在内部，每个掩码组件必须全部为 0 位或全部为 1 位。
让我们比较具有大于运算符的两个 AVX 浮点向量：
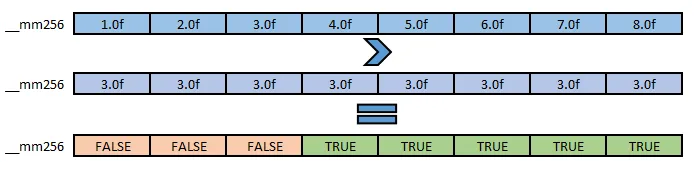
输入是两个带有浮点分量的向量。逻辑运算的输出也是一个带浮点分量的向量，但其值的位数被设置为全 0 或全 1。全 1 表示 “真”，全 0 表示 “假”。对于浮点数，全 1 的值打印为-nan，对于整数，则打印为-1。存储的实际值并不重要。我们只需要知道它保存的是真值和假值。
逻辑运算符的结果(>、<、==、&&、||等：以逻辑&&运算符为例：
vector && vector = maskmask && mask == maskvector && mask == ?????
最后一种情况，可能会有意想不到的结果，这就像试图做 3 > false，也许在 C++ 中这是可行的，但在逻辑意义上这是不正确的。
警告
注意：与布尔运算不同，并非零以外的任何数字都是 TRUE。只有所有位都设置为 1 的矢量成分才被视为 TRUE。不要使用其他值作为掩码。否则会失败，或得到意想不到的结果。
# 2. 条件加载
掩码可用于有条件地将值加载到向量中。比如可以使用掩码来有条件地控制值向量的加载：if_select(mask,value_true,value_false) 可以表示为：
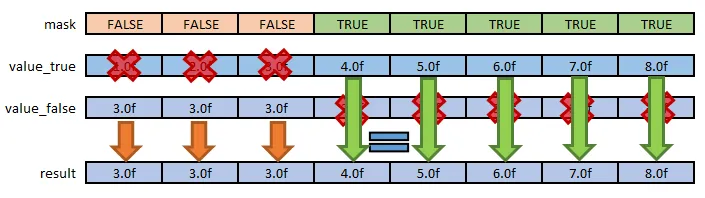
- 当掩码设置为
FALSE时，数据从value_false向量加载；当设置为TRUE时，数据从value_true向量加载。这个概念简单而有效。
注释
代码示例 1：使用掩码和 SIMD-Framework 中的 v8f.h 实现条件加载。（主要使用 if_select(mask,value_true,value_false) 方法，该函数是 _mm256_blendv_ps 的封装）
#pragma GCC optimize("O3", "unroll-loops", "omit-frame-pointer", "inline")
#pragma GCC option("arch=native", "tune=native", "no-zeroupper")
#pragma GCC target("avx")
#include <bits/stdc++.h>
#include <x86intrin.h>
#include "v8f.h"
using namespace std;
inline v8f testConditions(const v8f &value)
{
return if_select(value > 3.0f || (value <= -3.7f && value > -15.0f), sqrt(2.0f * value + 1.5f),
(-2.0f * value - 8.7f));
}
inline bool validate(const v8f &test, const v8f &vector)
{
for (int j = 0; j < 8; ++j)
{
float value = test[j];
float expected;
if (value > 3.0f || (value <= -3.7f && value > -15.0f))
{
expected = sqrt(2.0f * value + 1.5f);
}
else
{
expected = (-2.0f * value - 8.7f);
}
if (abs(expected - vector[j]) > 0.00001f)
{
cout << "Assert Error:" << expected << " " << vector[j] << endl;
return false;
}
}
return true;
}
int main()
{
int validTests = 0;
int TotalTests = 1000;
for (int i = 0; i < TotalTests; ++i)
{
float offset = -500.0f + (1000.0f * i) / TotalTests;
v8f test(1.4f, 3.3f, -12.5f, -33.4f, 7.9f, -70.2f, 15.1f, 22.6f);
test += offset;
v8f result = testConditions(test);
if (validate(test, result))
{
++validTests;
}
}
cout << "Valid Tests:" << validTests << "/" << TotalTests << " ("
<< (100 * validTests / TotalTests) << "%)" << endl;
if (validTests != TotalTests)
{
return -1;
}
return 0;
}
# 3. 性能
使用掩码的条件加载不是真正的分支，因此它们不会有误预测，并且 CPU 可以更好地利用无序执行。但这是有代价的。因为它们是无分支的，并且所有条件执行都是通过掩码操作完成的，所以总是计算和执行这两个分支。如果要对 value_false 进行非常复杂的计算，那么即使只有 0.00001% 的时间会发生，也会一直进行计算。如果代码中有些部分很少需要，但计算成本很高，这可能会导致性能问题。在下一章数据流控制中，可以通过控制数据流的方法，根据某些条件提前退出循环。
# 六、数据流控制
# 1. 共享数据流问题
在线性编程中，创建条件分支 if、switch、continue 和 break 来控制数据流没有任何问题。你只需创建一个无限循环，并在条件满足时跳出循环即可。但是一个向量不仅有一个条件结果，而且同时有 N 个条件结果。向量的一部分可以准备退出循环(因为向量数据已达到退出条件)，但其余数据在退出之前仍有活动工作要做。
警告
如果向量分量已经计算完成，请冻结它以避免对其进行任何进一步的计算。具体做法是在任何数值赋值中屏蔽已完成的分量。未完成的向量分量会不断更新，但已完成的分量不会。因此，如果我有一个 8x 浮点矢量，而分量 0、1、4 和 7 已达到结束状态，我就需要在每次数据加载时加上一个掩码[false,false,true,true,false,true,false]
# 2. 避免执行计算开销很大的分支
要节省 CPU 时间，最简单的方法是检查掩码内的所有值是否相同，要么全部为 “true”，要么全部为 “false”。当掩码内的所有值都相同时，我们就得到了一个简单的布尔值，要么为真，要么为假。这可以用来跳过部分代码，或使用普通的条件分支：if、switch、continue 和 break 等。
在 SIMD-Framework 中，使用的是 horizontal_or(mask)函数（封装了_xxx_testz_xx）。该函数检查掩码内是否有任何值为真，如果存在真值则返回 true，否则返回 false。
注释
代码示例 2：使用 horizontal_or(mask) 函数判断掩码内是否有任何值为真，减少分支计算
v8f result(0.0f);
for (int i = 0; i < 2000; i++)
{
v8f test(1.4f, 3.3f, -12.5f, -33.4f, 7.9f, -70.2f, 15.1f, 22.6f);
test += ((float)i) / 100.0f;
if (horizontal_or(test >= 38.0f))
{
result += if_select(test >= 38.0f, slowFunction(i), test);
}
else
{
// 全为 false，不需要执行 slowFunction，直接加上 test 向量即可
result += test;
}
}
- 通过使用
horizontal_or，还可以提前跳出循环。自动向量化无法实现这种优化，但手动向量化可以，而且是首选。
注释
代码示例 3：使用 horizontal_or 提前跳出循环，该程序需要同时进行 8 次并行模拟，以 200 个回合为限，计算最大连击得分。一旦在任何一次并行模拟中得分超过 1700 分，就结束模拟，并返回最大得分（一个浮点数值，不是包含所有得分的整个向量，只是最大值）和获得该得分的回合。
#pragma GCC optimize("O3", "unroll-loops", "omit-frame-pointer", "inline")
#pragma GCC option("arch=native", "tune=native", "no-zeroupper")
#pragma GCC target("avx")
#include <bits/stdc++.h>
#include <x86intrin.h>
#include "v8f.h"
using namespace std;
int validateResult(const int &turn, const float &bestScore)
{
cout << "Turn:" << turn << " bestScore:" << std::setprecision(10) << bestScore << endl;
if (turn != 133)
{
cout << "ERROR, Expected turn exit at 133 != " << turn << endl;
return -1;
}
if (bestScore != 1707.318481f)
{
cout << "ERROR, Expected a bestScore of 1707.318481f != " << std::setprecision(10)
<< bestScore << endl;
return -1;
}
return 0;
}
int main()
{
int turn = 0;
v8f Scores(1.0f, 3.0f, 7.0f, 13.4f, 22.7f, 0.01f, 4.556f, 9.7f);
for (turn = 0; turn < 200; ++turn)
{
Scores += ((float)(turn) / 15.0f);
if (turn == 40)
{
Scores *= Scores / 15.0f + 2.0f;
}
if (turn == 70)
{
Scores += if_select(Scores < 430.0f, 850.0f, 120.0f);
}
// 利用 horizontal_or 提前退出循环
if (horizontal_or(Scores >= 1700.0f))
{
break;
}
}
cout << "Scores: " << Scores << endl;
float bestScore = 0.0f;
// 遍历获取最大分量
for (int i = 0; i < 8; i++)
{
float score = get(Scores, i);
if (bestScore < score)
{
bestScore = score;
}
}
return validateResult(turn, bestScore);
}
# 七、数据对齐
数据对齐是一种强制编译器在特定字节边界的内存中创建数据对象的方法。这样做的目的是为了提高从处理器加载和存储数据的效率。无需赘述，当数据可以在特定字节边界的内存地址之间移动时，处理器就可以高效地移动数据。对于支持英特尔® AVX-512 指令的英特尔® 处理器来说，当数据起始地址位于 64 字节边界时，内存移动效果最佳。因此，需要强制编译器创建起始地址为 64 字节模的数据对象。
除了在对齐边界上创建数据（使基指针对齐）外，编译器还能在已知数据访问（包括基指针和索引）对齐 64 字节时执行优化。在通常情况下，如果没有用户的帮助，编译器并不知道循环内部的数据是对齐的。这可能迫使编译器在生成代码时采取保守做法，从而影响性能。因此还必须通过编译指示(C/C++)或指令(Fortran)、选项(如 Fortran 中的-Align array64byte)以及子句/属性的组合来通知编译器进行对齐，以便英特尔编译器能够生成最佳代码。
总而言之，需要两个步骤：
- 数据对齐
- 在性能关键区域(使用数据的区域)中使用 pragma/directives/clauses 来告诉编译器内存访问是对齐的
# 1. 数据对齐
调整数据以提高应用性能非常重要。这通常意味着两点：
- 在为数组（或指针）分配空间时对齐基指针
- 确保每个向量化循环（对于每个线程）的起始索引具有良好的对齐属性
对齐静态数组（基指针）
- 静态数组的对齐十分简单，不过在 Windows 上与 Linux 上的声明有所区别，以 64 字节边界上静态声明 1000 元素单精度浮点数组为例
- 在 Windows 上，使用
__declspec(align(64))修饰符：
__declspec(align(64)) float a[1000];
- 在 Linux 上，使用
__attribute__((aligned(64)))修饰符：
float a[1000] __attribute__((aligned(64)));
对齐动态数据
- 动态数据的对齐相对复杂，需要使用特殊的内存分配函数，如
_mm_malloc和_mm_free来替代malloc和free函数。其中，这些函数的第二个参数是对齐参数（以字节为单位），比如mm_malloc(p, 64)返回的数据将是 64 字节对齐的。
重要
对于动态分配的 C/C++ 数组，仅仅在创建时使用 mm_malloc 对齐数据是不够的（这是一个必要条件），还需要在相关循环之前添加一个__assume_aligned(a, 64) 形式的子句。如果没有这一步，编译器将无法检测使用此类数组进行访问时的最佳对齐方式。
- 在 C++17 中，还可以使用
std::aligned_alloc函数来分配对齐的内存，但是这个函数只能在 C++17 中使用，而且只能在 Linux 上使用。使用方式如下：
float *a = std::static_cast<float *>std::aligned_alloc(64, 1000 * sizeof(float));
// 使用完毕后，需要释放内存
std::free(a);
对齐循环索引
对于内存访问形式为 a[i+n1] 的循环，必须满足特定的对齐要求。具体来说，用户必须确保 （i-loop 的下界 + n1）是 16 的倍数（假设数据类型为 float）。
此外，除非在编译时信息可以在静态情况下获得（例如访问形式为 x[i] ，并且所有线程的循环下界都是常数 0，或者在循环内部存在形式为 b[i+16*k] 的访问），用户还必须通知编译器关于这个对齐要求。否则，这一步还需要在循环前添加一个 __assume(n1%16==0) 或者 #pragma vector aligned 的语句（ 仅限于 Windows 平台 ）。以下是一个不满足数据对齐要求的例子：
#define N 1000
float a[N] __attribute__((aligned(64)));
void process_array()
{
for (int i = 0; i < N; i++)
{
float result = a[i + 4]; // 访问 a[i+n1]，其中 n1 = 4
// 其它计算操作...
}
}
- 如果我们要确保内存访问的性能最佳，我们需要确保 i 和 n1 的组合是对齐的，以便在向量化指令集中能够更有效地执行。在上面的代码中，循环的下界是 i 的初始值 0 ，所以 (0 + 4) 不是 16 的倍数。为了满足对齐要求，我们需要进行调整，并且通知编译器这个对齐属性。
#define N 1000
float a[N] __attribute__((aligned(64)));
void process_array(int n1)
{
for (int i = 0; i < N; i += 16) // 调整循环的步长。
{
__assume((n1 % 16) == 0);
float result = a[i + n1]; // 访问 a[i+n1]
// 其它计算操作...
}
}
# 2. 通知编译器数据对齐
既然已经对齐了数据，那么在程序中实际使用数据时，就有必要告知编译器这些数据是对齐的。例如，将数据作为参数传递给性能关键的函数或子程序时，编译器如何知道参数是对齐的还是未对齐的？例如，数据通常在一个源文件中声明，但在许多其他源文件中使用。因此，这一信息必须由用户提供，因为编译器往往没有关于参数的信息。
有两种方法可以告知编译器数据对齐情况。 一种方法是使用 OpenMP SIMD ALIGNED 子句通知编译器在使用数据时的数据对齐情况。另一种方法则是使用英特尔专有子句在代码中指定数据对齐方式。
编译器要为 i 循环内的（浮点数组）内存访问（如 a[i+n1] 和 X[i]）生成对齐的加载/存储，就必须知道：
- 基数指针（a 和 X）已对齐。对于静态数组，可以使用上面讨论的技术实现对齐，例如使用
__declspec(align(64))。对于动态分配的数组，仅仅在创建时使用mm_malloc或aligned_alloc对齐数据是不够的，还需要如下所示的子句__assume_aligned(a, 64)。 - 编译器必须知道（i-loop 的下界 + n1）是 16 的倍数（假设数据类型为 float）。如果循环下界为 0 ，那么所需的信息就是 n1 是 16 的倍数。一种方法是添加一个 __assume(n1%16==0) 形式的子句。
注释
代码示例 4： 在 Windows 上使用 __assume_aligned 和 __assume 指令来告知编译器数据对齐情况。
// compile options: -O3 -xcore-avx512 -qopt-report-phase=vec -qopt-report=5 -qopt-report-file=stdout -restrict -c
// 该编译指令将生成一个名为 stdout 的文件，其中包含有关向量化的信息。
// restrict 关键字：提示编译器：在该指针的生命周期内，其指向的对象不会被别的指针所引用。
#define N 1000
__declspec(align(64)) float X[N], X2[N];
void foo(float * restrict a, int n, int n1, int n2)
{
__assume_aligned(a, 64);
__assume((n1 % 16) == 0);
__assume((n2 % 16) == 0);
for (int i = 0; i < n; i++)
{
X[i] += a[i] + a[i + n1] + a[i - n1] + a[i + n2] + a[i - n2];
}
for (int i = 0; i < n; i++)
{
X2[i] += X[i] * a[i];
}
}
# 八、总结
本文主要介绍了 SIMD 的基本概念，以及 SIMD 的优化思路，最后通过一些简单的示例代码，介绍了 SIMD 的使用方法。主要内容如下：
- 在代码中使用 SSE 和 AVX 指令的硬件和软件要求。
- 可用的向量数据类型。
- 有关如何检查自动向量化使用情况的信息，以及有关可自动向量化的循环的提示。
- C++中的 SSE/AVX 框架。
- 掩码和条件加载。
- 数据流控制。
- 数据对齐。
SIMD 的优势和劣势：
优势
- 与线性代码相比，潜在的性能提升 300%到 600%。
- 与在 GPU 级别进行向量化编程的 CUDA 相似。
劣势
- 性能取决于运行硬件。
- 当存在大量数据加载和卸载时，性能不佳。
- 数据流会变得很难控制，而且向量内每个值的执行时间都会影响整个向量的执行时间。在所有值都满足退出条件之前，不能提前退出。
- 编码复杂。
- 缺乏内置函数： 三角函数、随机数、整数除法等。
总的来说，SIMD 的优势远大于劣势，SIMD 的使用可以大大提高程序的性能，但是需要注意的是，SIMD 的使用需要编码复杂，而且需要硬件支持，所以在使用 SIMD 之前，需要对程序进行分析，判断是否有必要使用 SIMD。
# 参考资料
[1] Introduction to SIMD instructions
[2] Agner Fog’s instruction tables
[3] Intel C++编译器的矢量化
[6] libdivide
[7] Avoiding AVX-SSE Transition Penalties
[8] Why is this SSE code 6 times slower without VZEROUPPER on Skylake?