从生物物理学的角度来看,动作电位是通过细胞膜中离子通道的电流的结果。在对乌贼的巨型轴突进行的一系列广泛实验中,霍奇金和胡克斯利成功地测量了这些电流,并以微分方程的方式描述了它们的动力学。在转向 Hudgkin-Huxley 方程之前,我们需要补充一些关于离子通道平衡电位的额外知识。
# 一、平衡电位(Equilibrium Potential)
神经元和其他细胞一样,被一个膜所包围,该膜将细胞的内部与细胞外空间分开。细胞内的离子浓度与周围液体中的离子浓度不同。浓度的差异产生了一个电位,在神经元动力学中起着重要作用。该小节将对平衡电位给出一个直观的解释。
# 1. Nernst 电位(Nernst Potential)
根据热力学理论,分子处于能量状态的概率与 Boltzmann 因子成正比,即 $p \propto \exp \left( -E/kT \right )$,其中 $E$ 是分子的能量,$k$ 是 Boltzmann 常数,$T$ 是温度。现在考虑带有电荷 $q$ 的正离子在静电场中。它们在位置 $x$ 的能量为 $E=q u(x)$,其中 $u(x)$ 是 $x$ 处的电势。因此,正离子在位置 $x$ 附近的概率为 $p(x) \propto \exp \left[ -q u(x)/kT \right ] $。对于带有正电荷 $q>0$ 的离子,离子密度在电位低的区域更高。我们用 $n(x)$ 表示点 $x$ 处的离子密度。则点 $x_1$ 处和点 $x_2$ 处的密度之间的关系为:
$$ \frac{n(x_1)}{n(x_2)} = \exp \left [ -\frac{qu(x_1)-qu(x_2)}{kT} \right ] \tag{1.1} $$
因此,电位差 $\Delta u = u(x_1) − u(x_2)$ 引起了离子密度的差异。
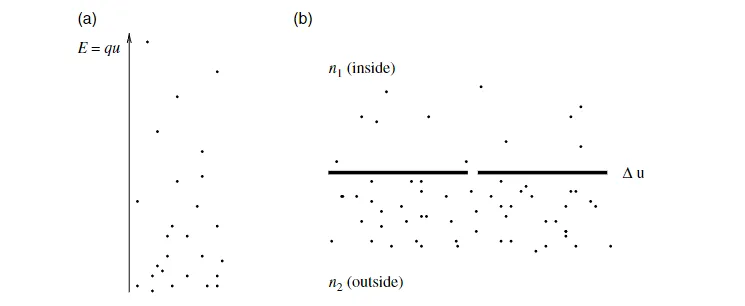
图 1.1: (a)在热平衡状态下,电场中的正离子分布为:高能态的离子较少,低能态的离子较多。因此,电压差会产生浓度梯度。(b) 类似地,离子浓度的差异会产生电势差。神经元内部的浓度与周围的浓度不同。由此产生的电位称为 **Nernst 电位** 。实线表示细胞膜。离子可以通过间隙传递。
由于这是关于平衡状态的陈述,反过来也是成立的。离子密度的差异会产生电势差 $\Delta u$ 。我们考虑两个离子浓度分别为 $n_1$ 和 $n_2$ 的区域;参见图 1.1(b)。通过求解公式 (1.1) 得到 $\Delta u$,我们发现,在平衡状态下,浓度差异会产生一个电压。
$$ \Delta u = \frac{kT}{q} \ln \frac{n_1}{n_2} \tag{1.2} $$
该电压又被称为 Nernst 电位(Hille, 2001)。
# 2. 反转电位(Reversal Potential)
细胞膜由一层薄的脂质双层组成,几乎是一个完美的电绝缘体。然而,在细胞膜中嵌入了特定的蛋白质,它们作为离子门控通道。第一种类型的门控通道是离子泵,第二种是离子通道。离子泵能够主动地将离子从一侧运输到另一侧。因此,细胞内液体中的离子浓度与周围环境不同。例如,哺乳动物神经元内的钠浓度(约为 $10 mM$ )低于细胞外液体中的钠浓度(约为 $145 mM$ )。另一方面,细胞内的钾浓度(约为 $140 mM$ )高于周围环境中的钾浓度(约为 $5 mM$ )。对于霍奇金和哈克斯利研究的鱿鱼巨大轴突,这些数字略有不同,但基本思想是相同的:细胞外的钠离子比细胞内多,而钾离子则相反。
让我们暂时专注于钠离子。在平衡状态下,浓度差引起了约为 $+67 mV$ 的 Nernst 电位 $E_{Na}$ 。也就是说,在平衡状态下,细胞内部相对于周围环境具有正电势。细胞内部和周围液体通过离子通道相互联系,钠离子可以从膜的一侧通过到另一侧。如果电压差 $\Delta u$ 小于 Nernst 电势 $E_{Na^{+}}$ 的值,更多的 $Na^+$ 离子会流入细胞,以减小浓度差异。如果电压大于 Nernst 电势,离子会从细胞流出。因此,当电压 $\Delta u$ 通过 $E_{Na}$ 时,电流的方向会反转。因此,$E_{Na}$ 被称为反转电位。
继续看钾离子,正如上面提到的,钾离子在细胞内的浓度(约为 $140 mM$ )比细胞外液体(约为 $5 mM$ )高。钾离子具有单个正电荷 $q = 1.6 × 10^{-19} C$ 。应用 Nernst 公式(1.2),其中玻尔兹曼常数 $k = 1.4 × 10^{-23} J/K$ ,在室温下得到 $E_K ≈ -83 mV$ 。因此,钾离子 $K^{+} 的反转电势是负的。
到目前为止,我们考虑了钠或钾的存在。在真实的细胞中,这些和其他离子类型同时存在,并对跨膜电压做出贡献。实验发现,细胞膜的静息电位约为 $u_{rest} ≈ 65 mV$ 。由于 $E_K < u_{rest} < E_{Na}$ ,钾离子在静息电位下从细胞流出,而钠离子则流入细胞。在稳态下,主动离子泵平衡这种流动,并通过通道运输与通过通道的离子数量相同的离子返回。$u_{rest}$ 的值由通道中离子流动(膜的渗透性)和主动离子转运(维持浓度差的离子泵的效率)之间的动态平衡决定。
# 二、Hudgkin-Huxley 模型
霍奇金和哈克斯利(1952)对乌贼的巨型轴突进行了实验,发现了三种不同类型的离子电流,即钠、钾和主要由氯离子组成的泄漏电流。特定的电压依赖性离子通道,一个用于钠,另一个用于钾,控制这些离子通过细胞膜的流动。泄漏电流负责其他未明确描述的通道类型。
# 1. 模型定义(Model Definition)
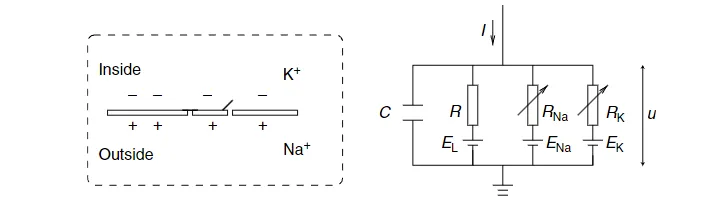
图 2.1: Hodgkin-Huxley 模型示意图。
Hodgkin-Huxley 模型可以通过图 2.1 来理解。半透膜细胞膜将细胞内部与细胞外液体隔开,并起到电容器的作用。如果将输入电流 $I(t)$ 注入细胞,它可能会在电容器上增加进一步的电荷,或者通过细胞膜中的通道泄漏。
图 2.1 中的每种通道类型都由一个电阻器表示。非特异通道具有泄漏电阻 $R$ ,钠通道具有电阻 $R_{Na}$ ,钾通道具有电阻 $R_K$ 。电阻器图中的对角箭头表示电阻值不固定,而是根据离子通道是否打开或关闭而变化。
由于通过细胞膜的主动离子转运,细胞内的离子浓度与细胞外液体不同。由离子浓度差产生的 Nernst 电位在图 2.1 中由电池表示。由于每种离子类型的 Nernst 电位不同,分别为钠、钾和非特异第三通道设置了单独的电池,其电池电压分别为 $E_{Na}$ 、$E_K$ 和 $E_L$ 。
现在让我们将上述电路图转化为数学方程。膜上电荷的守恒意味着施加的电流 $I(t)$ 可以分为充电电流 $I_C$ ,用于充电电容器 $C$ ,以及通过离子通道的其他电流 $I_k$ 。因此,可以写成以下方程:
$$ I(t) = I_C(t) + \sum_{k} I_k(t) \tag{2.1} $$
在标准的 Hodgkin-Huxley 模型中,只有三种类型的通道:一个带有 $Na$ 索引的钠通道,一个带有 $K$ 索引的钾通道,以及一个具有电阻 $R$ 的非特异泄漏通道。根据电容的定义 $C = q / u$ ,可以得到充电电流 $I_C = C\frac{du}{dt}$ 。因此,方程 (2.1) 可以写成:
$$ C \frac{du}{dt} = I(t) - \sum_{k} I_k(t) \tag{2.2} $$
在生物学术语中,$u$ 是膜上的电压,$\sum_{k} I_k(t)$ 是通过细胞膜的离子电流之和。
如上所述,Hodgkin-Huxley 模型描述了三种类型的通道。所有通道可以通过它们的电阻或等效地通过它们的电导来表征。泄漏通道由电压无关的电导 $g_L=1/R$ 来描述。由于 $u$ 是细胞膜上的总电压,$E_L$ 是电池的电压,在图 2.1 中泄漏电阻器的电压为 $u - E_L$ 。根据欧姆定律,我们得到泄漏电流 $I_L = g_L (u - E_L)$ 。
其他离子通道的数学模型类似,只是它们的电导是电压和时间依赖的。如果所有通道都打开,它们分别以最大电导率 $g_{Na}$ 或 $g_K$ 发射电流。然而,通常情况下,一些通道被阻断。霍奇金和哈克斯利的突破是,他们成功地测量了通道的有效电阻如何随着时间和电压的变化而变化。此外,他们还提出了对其观察结果的数学描述。具体来说,他们引入了额外的门控变量 $m$ , $n$ 和 $h$ 来模拟模拟通道在给定时间点开放的概率。例如,钠通道的有效电导被建模为 $1 / R_{Na} = g_{Na} \cdot m^3 h$ ,其中 $m$ 描述通道的激活(开放),$h$ 描述通道的失活(阻塞)。钾的电导率为 $1 / R_K = g_K \cdot n^4$ ,其中 $n$ 描述通道的激活。
总的来说,霍奇金和哈克斯利将公式 (2.2) 右边的三个离子电流写成:
$$ \sum_{k} I_k(t) = g_{Na} \cdot m^3 h \cdot (u - E_{Na}) + g_K \cdot n^4 \cdot (u - E_K) + g_L \cdot (u - E_L) \tag{2.3} $$
其中参数 $E_{Na}$ , $E_K$ , 和 $E_L$ 是反转电位。
三个门控变量 $m$ , $n$ 和 $h$ 根据以下形式的微分方程变化:
$$ \dot{x}=-\frac{1}{\tau_x (u)}\left [ x-x_0(u)\right ] \tag{2.4} $$
其中,$\dot{x} = \frac{dx}{dt}$ ,其中 $x$ 表示 $m$, $n$ 或者 $h$ 。公式 (2.4) 的解释很简单:对于一个固定的电压 $u$ ,变量 $x$ 以时间常数 $\tau_x(u)$ 逼近目标值 $x_0(u)$ 。目标值 $x_0(u)$ 和时间常数 $\tau_x(u)$ 对电压的依赖关系分别如图 2.2 (a), (b) 所示。
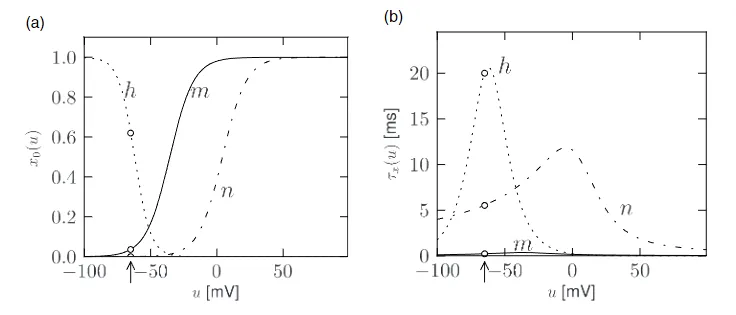
图 2.2 : Hodgkin-Huxley 模型。(a) 门控变量 $m$, $n$, $h$ 的平衡函数。(b)与电压有关的时间常数,静息电位为 $u=-65mV$ (箭头),参数由表 2.1 给出。

表 2.1 :在大脑皮层上的锥体神经元上拟合的 Hodgkin-Huxley 方程的参数。$n$ 和 $m$ 的参数由 Zach Mainen(Mainen et al., 1995)根据 Huguenard 等人(1988)报告的实验进行拟合,$h$ 的参数由 Richard Naud 根据 Hamill 等人(1991)报告的实验进行拟合。电压以 $mV$ 为单位,膜电容为 $C = 1 \mu F/ cm^2$ 。
图 2.2 中绘制的函数形式,以及公式(2.3)中的最大电导和反转电位,是霍奇金和哈克斯利根据经验推导出来的。
实验者通过向细胞注入适当的电流来保持细胞膜上的电压在所需的值上。在实验中,假设实验者在 $t<t_0$ 时将细胞保持在静息电位 $u_0 =-65mV$ ,并且在 $t=t_0$ 时将电压切换到一个新值 $u_1$ 。对于 $t > t_0$ ,通过对微分方程(2.4)进行积分,可以得到以下动力学方程:
$$ \begin{aligned} & m(t)=m_0(u_1) + [m_0(u_0)-m_0(u_1)] \exp \left[ -\frac{t-t_0}{\tau_m(u_1)} \right ] ,\\ & h(t)=h_0(u_1) + [h_0(u_0)-h_0(u_1)] \exp \left[ -\frac{t-t_0}{\tau_h(u_1)} \right ] , \end{aligned} \tag{2.5} $$
其中 $m(t)$ 和 $h(t)$ 分别表示钠通道和钾通道的激活和失活状态。基于给定的函数 $m_0(u)$ 、$h_0(u)$ 、$\tau_m(u)$ 和 $\tau_h(u)$ 的模型,可以预测在 $t > t_0$ 时电压变化引起的钠电流 $I_{Na}(t)=g_{Na} [m(t)^3] h(t) (u_1 - E_{Na})$ 和钾电流 $I_K(t)=g_K [n(t)^4] (u_1 - E_K)$ 。
而 $n(t)$ 的表达式为:
$$ n(t)=n_0(u_1) + [n_0(u_0)-n_0(u_1)] \exp \left[ -\frac{t-t_0}{\tau_n(u_1)} \right ] \tag{2.6} $$
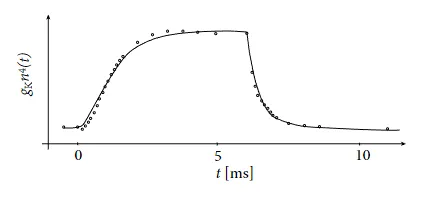
图 2.3 :Hodgkin 和 Huxley 绘制的钾离子电导率变化原始测量曲线和公式拟合曲线。施加 $25 mV$ 的电压切换后,回到静息电位后,钾的电导率(圆圈)的测量时间过程。拟合实线是基于公式(2.6)的。
霍奇金和哈克斯利使用方程(2.4)和(2.5)反过来进行研究。他们在使用适当的药物阻断钠通道后,施加电压变化并测量钾电流的时间变化。将记录的电流除以驱动电位 $(u_1 - E_K)$ 可以得到时间相关的电导率 $g_K [ n(t)^4]$ (图 2.3 )。使用方程(2.6),霍奇金和哈克斯利推导出了钾通道的 $n_0(u_1)$ 和 $τ_n(u_1)$ 的值,以及 $n^4(t)$ 中的指数 4。通过对不同的 $u_1$ 值重复实验,可以得到 $n_0(u)$ 和 $τ_n(u)$ 的实验曲线。
变量 $m$ 被称为激活变量。为了理解这个术语,我们注意到从图 2.2 可以看出,在神经元的静息电位 $u = -65 mV$ 时,$m_0(u)$ 的值接近于零。因此,在静息状态下,通过通道的钠电流 $I_{Na} = g_{Na} m^3 h(u - E_{Na})$ 为零。换句话说,钠通道是关闭的。
当膜电位显著增加超过静息电位时,门控变量 $m$ 增加到其新值 $m_0(u)$ 。只要 $h$ 不变,钠电流就会增加,门打开。因此,变量 $m$ “激活”了通道。如果在电压恢复到静息状态后,$m$ 衰减回零,就被称为“去激活”。类似地,关于失活变量 $h$ 的术语也是类似的。在静息状态下,$h$ 有一个较大的正值。如果电压增加到超过 $-40 mV$ 的值,$h$ 接近一个接近静息状态的新值 $h_0(u)$ 。因此,通道通过一个由 $\tau_h(u)$ 给出的时间常数“失活”(阻塞)。如果电压返回到零,$h$ 增加,使得通道经历“去失活”。这听起来像是一种棘手的词汇,但事实证明,将一个去激活的通道($m$ 接近零,$h$ 接近 1)与一个失活的通道($h$ 接近零)区分开来是有用的。
# 2. 随机通道的打开(Stochastic Channel Opening)
首先,离子通道的数量在一个细胞膜上是有限的,而且每个离子通道的开启和关闭是随机的。因此,当实验者记录通过细胞膜的电流时,他不会发现测量变量随时间平滑可靠地演变,而是会发现电流高度波动,每次重复实验时看起来都不同。这就是离子通道的随机性(如图 2.4 所示)。
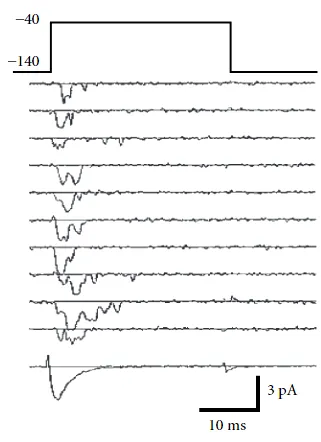
图 2.4 : 随机通道激活现象。在实验中,当施加一个电压阶跃到细胞膜上时,通过细胞膜的电流会呈现阶梯状变化,并且在每次试验中都有所不同(如顶部的连续轨迹所示)。对多次试验进行平均后,得到的结果是底部的轨迹。
然而,Hodgkin-Huxley 模型是用确定性方程描述离子通道的开启和关闭的。这些方程涉及的变量包括 $m$ ,$h$ 和 $n$ ,它们对应的是通过一个假设的、包含无限数量离子通道的极大细胞膜的电流密度,或者说是通过一小片细胞膜的电流,但是这个电流是在多次重复同一实验后得到的平均值。这就是 $Hodgkin-Huxley$ 模型的局限性,因为它忽略了离子通道的随机性。不过可以通过向模型中添加适当的噪声来包含随机性。这种噪声可以模拟离子通道开启和关闭的随机性,从而使模型更准确地描述神经元的动力学行为。
使用以电压为自变量的转换速率 $\alpha$ 和 $\beta$ 来描述每种通道类型的激活和失活动力学,公式如下:
$$ \begin{aligned} \dot{m}= &\alpha_m (u) (1-m) - \beta_m (u) m ,\\ \dot{n}= &\alpha_n (u) (1-n) - \beta_n (u) n ,\\ \dot{h}= &\alpha_h (u) (1-h) - \beta_h (u) h , \\ \end{aligned} \tag{2.7} $$
公式 (2.4)和 (2.7)是等价的。逼近值 $x_0(u)$ 和时间常数 $\tau_x(u)$ 由变换 $x_0(u)=\alpha_x(u)/[\alpha_x(u)+\beta_x(u)]$ 和 $\tau_x(u)=1/[\alpha_x(u)+\beta_x(u)]$ 给出。表 2.1 中的第二个表格给出了各种以 $u$ 为自变量的经验拟合函数 $\alpha$ 和 $\beta$ ,用于生成图 2.2 中的曲线。
方程(2.7)是化学中常用的方程,用于描述具有速率常数 $α$ 和 $β$ 的激活过程的随机动力学。我们可以将这个过程解释为具有电压依赖的转换速率的两个状态之间的分子开关。例如,激活变量 $n$ 可以解释为找到一个开放的钾通道的概率。因此,在一个具有 $K$ 个离子通道的细胞膜中,预计有 $k \approx (1 - n)K$ 个通道是关闭的。我们可以将 $\alpha_n(u) \Delta t$ 解释为在短时间区间 $\Delta t$ 内,暂时关闭的通道中有一个切换到开放状态的概率。
# 3. Hudgkin-Huxley 模型的动力学(Dynamics of Hudgkin-Huxley Model)
不同类型的输入被依次考虑,包括脉冲输入、恒定输入、阶跃电流输入和时间依赖输入。选择这些输入场景是为了直观理解 Hodgkin-Huxley 模型的动力学特性。Hodgkin-Huxley 模型最重要的特性是能够产生动作电位。在图 2.5(a) 中,一个持续 $1ms$ 的短脉冲电流在 $t=1ms$ 时施加,引发了一个动作电位。这个脉冲的幅度接近 $100mV$ ,半峰宽约为 $2.5ms$ 。在动作电位之后,膜电位下降到静息电位以下,再慢慢回到静息电位值 $-65mV$ 。
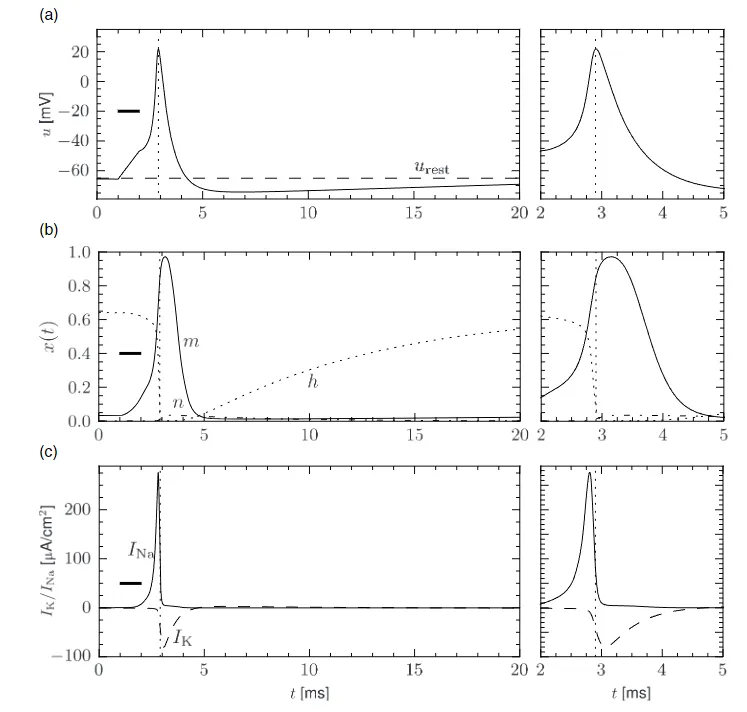
图 2.5 : (a)动作电位。Hodgkin-Huxley 模型受到 $t=1ms$ 和 $t=2ms$ 之间的短而强的电流脉冲的刺激。对于 $t>2ms$ 的膜电位 $u(t)$ 的时间变化显示了动作电位(正峰值),随后是相对不应期,此时电位低于静息电位 $u_{rest}$(虚线)。右侧面板显示了 $t=2ms$ 和 $t=5ms$ 之间动作电位的放大视图。(b)门控变量 $m,h,n$ 的变化揭示了动作电位是如何通过钠通道和钾通道介导的。(c)钠电流 $I_{Na}$ 取决于变量 $m$ 和 $h$ ,在动作电位的上升阶段有一个脉冲。钾电流 $I_K$ 受变量 $n$ 控制,并与 $I_{Na}$ 相比有一定的延迟开始。
- 脉冲产生过程中离子通道的动力学(Ion channel dynamics during spike generation) 为了理解动作电位生成的生物物理学基础,我们回到图 2.2(a) 。我们发现 $m_0$ 和 $n_0$ 随着 $u$ 的增加而增加,而 $h_0$ 则减少。因此,如果某些外部输入导致膜电压上升,由于 $m$ 的增加,钠通道的电导增加。结果,正钠离子流入细胞,进一步提高膜电位。如果这种正反馈足够大,就会引发动作电位。当膜电位接近钠电流的反转电位 $E_{Na}$ 时,这种爆发性增加自然停止。
在高 $u$ 值下,由于因子 $h$ 的作用,钠电导缓慢关闭。如图 2.2(b) 所示,时间常数 $\tau_h$ 始终大于 $\tau_m$ 。因此,使通道失活的变量 $h$ 对电压增加的反应比激活通道的变量 $m$ 慢。在类似的较慢时间尺度上,钾电流在图 2.5(c) 中开始。由于它是向外的电流,它降低了电位。钠和钾电流的整体效应是一个短暂的动作电位,随后是负超调;(负超调,又被称为超极化脉冲后电位,是由于 $h$ 变量引起的钠通道的缓慢去失活过程所导致)。
Hudgkin-Huxley 模型的动力学覆盖的知识比较多,主要概念如下:
- 平均发射率与增益函数(Mean Firing Rate and Gain Function)
- 时间依赖的输入刺激 (Stimulations by Time-Dependent Input)
- 发射阈值(Firing Threshold)
- 不应性(Refractoriness)
- 阻尼振荡与瞬时脉冲(Damped Oscillations and transient spiking)
这里就不继续介绍了,有兴趣的可以参考原文。
# 参考文献
- [1] Gerstner, Wulfram, Werner M. Kistler, Richard Naud, and Liam Paninski. Neuronal dynamics: from single neurons to networks and models of cognition. Cambridge university press, 2014.
