# 一、神经元系统的结构
生物神经元是一种高度特化的细胞,其结构和功能包含很多因素,其中神经元的几何形态特征和电学物理特性是两个重要方面。几何形态特征主要指神经元的空间结构,而电学物理特性包含神经元不同的动作点位发放模式。生物神经系统内有两类细胞:神经元细胞和神经胶质细胞,前者担负着信息处理的主要任务,而后者对前者起支持作用。神经元细胞的几何形态结构和电学物理特性是生物神经系统进行信息处理的基础。所谓的神经胶质细胞,它们是脑组织能量供应和结构稳定所需要的。由于胶质细胞不直接参与信息处理,本文将不再进一步讨论它们。本文还将忽略一些罕见的神经元亚型,如哺乳动物视网膜上的非脉冲神经元。本文只专注于脉冲神经元。
# 1. 理想的脉冲神经元 (ideal spike neuron)
一个典型的神经元可以分为三个功能不同的部分,称为树突(dendrite)、细胞体(soma)和轴突(axon)。
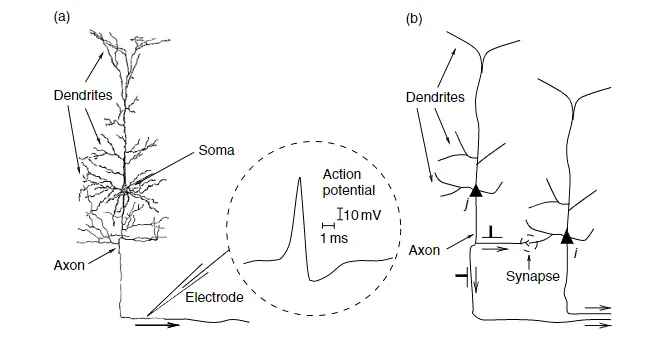
图 1.1:(a) Ramón y Cajal 于 1899 年绘制的神经元示意图。树突、体细胞和轴突可以被清楚地区分出来。图片显示了一个神经元动作电位的例子。动作电位是一个持续时间为 $1ms$ 的短电压脉冲,振幅约为 $100mv$ 。(b) 从突触前神经元 $j$ 到突触后神经元 $i$ 的信号传输。突触由虚线圈标记。右下端的轴突通向其它神经元。
- 树突:指从神经元细胞体内向外伸出的许多较短的分支,它们充当着神经元的输入端,接收来自其它神经元的神经冲动并传递给细胞体;
- 细胞体:神经元的核心,由细胞核、细胞质和细胞膜等组成,负责处理接收到的信号;
- 轴突:指由神经元细胞体向外伸出的一条最长的分支,它是管状纤维组织,充当神经元的输出端,再轴突末端有很多神经末梢,它们向外发出神经冲动。
神经元的轴突末梢经过多次分支,最后每一个小支的末端膨大呈杯状或球状,称为突触小体。这些突触小体可以与多个神经元的细胞体或树突相接触,形成神经元之间连接的突触(synapse)。通常把发送神经元成为突触前神经元(presynaptic neuron),把接收神经元称为突触后神经元(postsynaptic neuron)。
# 2. 脉冲序列 (spike train)
生物神经系统在内外刺激作用下,使得神经元按照一定的时间间隔产生一系列的活动电位,称为脉冲序列 (spike train)。神经元信号由短的电脉冲组成,可以通过在神经元的体部或靠近体部或轴突的位置放置一个精细的电极来观察,如下图所示,脉冲(或活动电位),其振幅为 100 毫伏,通常持续时间为 1~2 ms。脉冲的形式不会因为活动电位沿轴突传播而改变。神经元发送的单个活动电位或脉冲是信号传递的基本单元,因为所有脉冲的波形都是相似的,所以活动电位的形状不会携带任何信息,而传递有用神经信息的是脉冲的发放时间和频率。
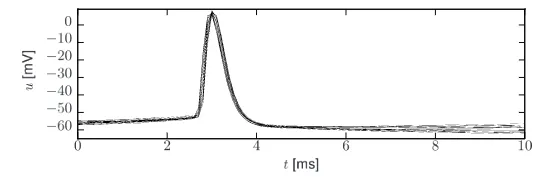
图 1.2:动作电位是刻板事件。在最大电压时间内排列的膜电位记录显示动作电位形状的变化很小。
脉冲序列中的活动电位通常是很好地分开的。即使有非常强的输入,也不可能在第一次脉冲期间紧接着激发第二次脉冲。两个脉冲之间的最小距离定义了神经元的绝对不应期(absolute refractory period)—— 大致在活动电位的复极化阶段(repolarization phase),无论用任何强的刺激都不能再引起活动电位。
# 3. 突触 (synapse)
突触前神经元的轴突与突触后细胞的树突(或体细胞)接触的部位是突触。脊椎动物大脑中最常见的突触类型是化学突触。在化学突触处,轴突终端非常接近突触后神经元,在突触前和突触后细胞膜之间只留下一个微小的间隙。这就是所谓的突触间隙(synaptic cleft)。当一个活动电位到达突触时,它触发了一个复杂的生化处理步骤链,导致神经递质从突触前末端释放到突触间隙中。一旦递质分子到达突触后一侧,它们将被突触后细胞膜上的专门受体检测到,并导致(直接或通过生化信号链)打开特定通道,导致细胞外液体中的离子流入细胞。离子的涌入反过来又改变了突触后部位的膜电位,因此,最后,化学信号被转化为电反应。从突触前神经元传入的脉冲信号引起突触后神经元膜电位发生的变化称为突触后电位(postsynaptic potential)。
除了化学突触之外,神经元还可以通过电突触连接,称为间隙连接(gap junctions)。特化膜蛋白在两个神经元之间形成直接的电连接。关于间隙连接的功能方面当前所知不多,但它们被认为参与了神经元的同步。
# 二、神经动力学的要素
脉冲对突触后神经元的影响可以用细胞内电极来记录,该电极测量细胞内部和其周围环境之间的电位差 $u(t)$ 。这个电位差被称为膜电位。在没有任何输入的情况下,神经元处于静息状态,对应一个恒定的膜电位 $u_{rest}$,称为静息电位(resting potential),一般在 $-80\sim -40mV$ (当以细胞外的电位为 0 )。当神经元受到外界刺激,突触后电位的总和超过某一阈值时,神经元产生一个不衰减的沿神经纤维传递的神经冲动,即活动电位或脉冲。活动电位的动态变化过程包含一个迅速的去极化正向电位变化和缓慢的复极化负向电位变化。活动电位的另一特征是电位的极性在峰电位顶端倒转,细胞内由静息时的负电位变为正电位,这一过程称为超射。神经元活动电位的产生会导致局部的兴奋性发生一系列的变化。大致在活动电位的复极化阶段(repolarization phase),无论用任何强的刺激都不能再引起活动电位,这个阶段称为绝对不应期(absolute refractory period);在随后的短时间内,活动电位进入超极化阶段(hyperpolarization phase),用比原来强的刺激方能引起活动电位,而且反应幅度还会小一些,这个阶段称为相对不应期(relative refractory period)。神经元对信号的传递方式在很大程度上与神经元的电学特性有关。
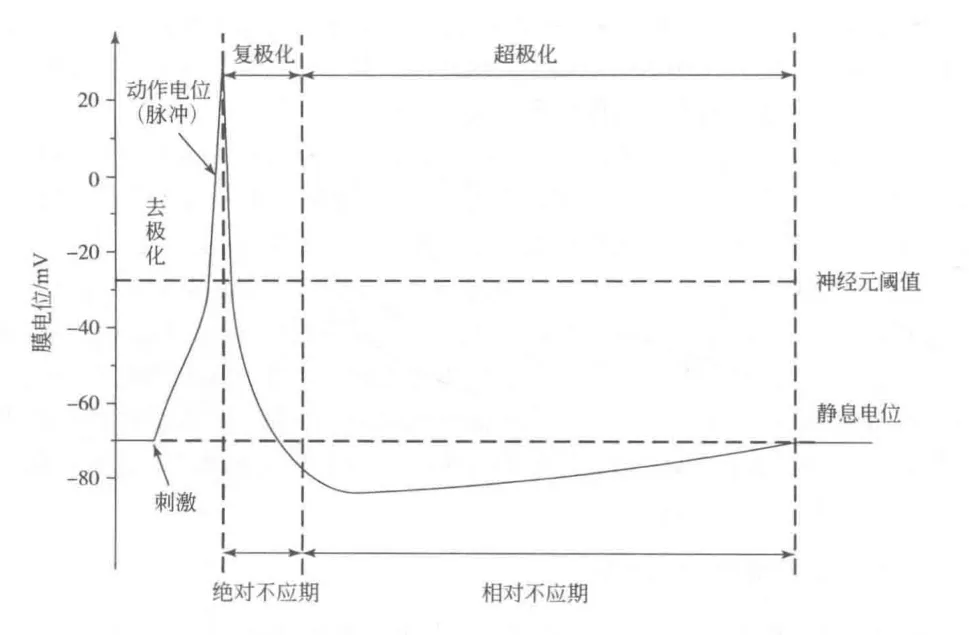
图 2.1:膜电位在绝对不应期和相对不应期的变化。在绝对不应期,神经元不能再次激发。在相对不应期,神经元可以激发,但需要更强的刺激。
# 1. 突触后电位(postsynaptic potential)
从突触前神经元传入的脉冲信号引起突触后神经元膜电位发生的变化称为突触后电位(postsynaptic potential),具有局部电位的性质。一个神经元通常有许多突触,其中有些是兴奋性的,有些是抑制性的。对于从突触前神经元传来的多个脉冲,由于突触类型的不同,突触后电位可分为兴奋性和抑制性两类。兴奋性突触使突触后神经元的膜去极化,产生正的突触后电位,称为兴奋性突触后电位(excitatory postsynaptic potential,EPSP)。EPSP 在传入脉冲到达突触后神经元 $0.3\sim 0.5ms$ 之后产生,它有一个较快的上升过程和缓慢的指数衰减过程,电位总共持续 $10\sim 20ms$ 。抑制性突触使突触后神经元的膜超极化,产生负的突触后电位,称为抑制性突触后电位(inhibitory postsynapticpotential,IPSP),IPSP 到达峰值时间和 EPSP 相似。
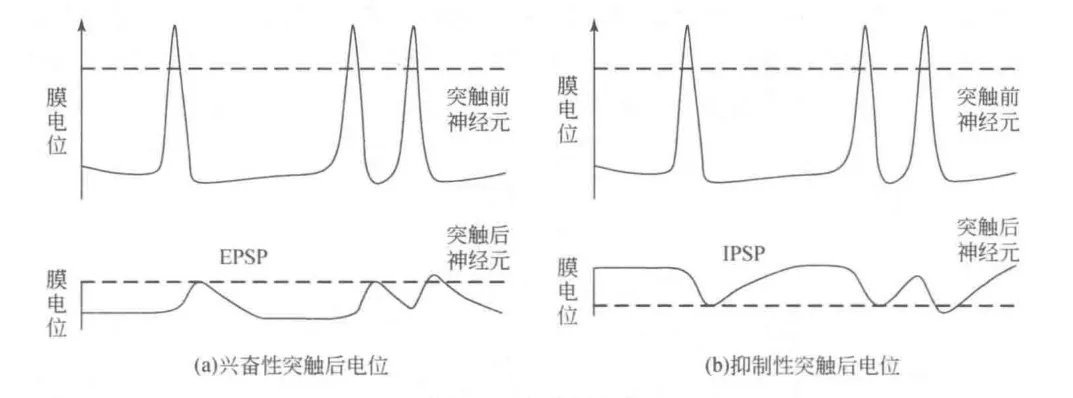
图 2.2:(a)兴奋性突触后电位(EPSP); (b)抑制性突触后电位(IPSP)。
用数学术语规范化,那么研究神经元 $i$ 的膜电位随时间变化的函数 $u_i(t)$ 。在输入脉冲到达之前,有 $u_i(t)=u_{rest}\ (t=0)$ 。对于 $t>0$ ,在电极上看到神经元 $i$ 的反应如下:
$$ u_i(t)-u_{rest}=: \varepsilon_{ij}(t) \tag{2.1} $$
# 2. 发射阈值与活动电位(firing threshold and action potential)
考虑两个突触前神经元 $j=1,2$ ,它们都向突触后神经元 $i$ 发送脉冲。神经元 $j=1$ 在时刻 $t_1^{(1)}, t_2^{(2)}, \cdots$ 发送脉冲,神经元 $j=2$ 也在时刻 $t_1^{(1)}, t_2^{(2)}, \cdots$ 发送脉冲。每个脉冲分别引起一个突触后电位 $\varepsilon_{i1}$ 或 $\varepsilon_{i2}$ 。只要只有少数的输入脉冲,电位的总变化大小约是各个 PSP 的总和:
$$ u_i(t)=\sum_{j}\sum_{f} \varepsilon_{ij}(t-t_j^{f}) + u_{rest} \tag{2.2} $$
即,膜电位对输入脉冲的反应是线性的。
另一方面,如果在很短的时间间隔内有太多的输入脉冲到达,线性就会被打破。一旦膜电位达到一个临界值 $\vartheta$ ,它的曲线就会显示出与 PSP 的简单求和完全不同的行为:膜电位表现出类似脉冲的偏移,振幅约为 $100 mV$ 。这个短电压脉冲将沿着神经元轴突与其他神经元的突触传播。在脉冲之后,膜电位并不直接回到静止电位,而是在许多神经元类型中通过低于静止值的超极化阶段。
单个 EPSP 的振幅在 $1 mV$ 的范围内。脉冲初始临界值比静息电位高约 $20$ 至 $30 mV$ 。因此在大多数神经元中,如下图所示的四个脉冲是不足以触发一个活动电位的。相反地,需要大约 $20\sim 50$ 个突触前脉冲在很短的时间窗口内到达才能触发一个突触后活动电位。这个时间窗口称为发射阈值(firing threshold),它是神经元的一个重要参数。
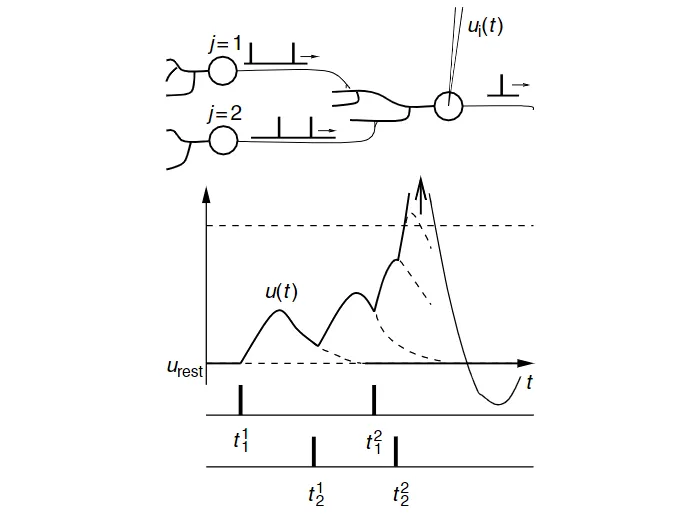
图 2.3:来自第二个突触前神经元 $j=2$ 的输入脉冲在来自神经元 $j=1$ 的尖峰后不久到达,导致第二个突触后电位增加到了第一个上。
# 三、Integrade-and-fire 模型
神经元动力学可以被视为一个整合的过程,与出发活动电位超过某个临界电压的机制相结合。事实上,在实验中,发射时间通常被定义为膜电位从下往上达到某个阈值的时刻。为了建立一个神经元动力学的现实模型,我们通过阈值 $\vartheta$ 来描述神经元的发射阈值。如果电压 $u_i(t)$ (包含所有输入的总效应)从下往上到达 $\vartheta$ ,我们就说神经元会发射一个脉冲。跨越阈值的时刻定义了发射时间 $t_i^f$ 。
该模型利用了一个事实,即一个而给定的神经元的活动电位总是具有大致相同的形式。如果一个活动电位的形状总是相同的,那么这个形状就不能用来传递信息;相反,信息包含在脉冲的存在或不存在中。因此活动电位被简化为“发生在一个精确的时刻的事件”。
将活动电位描述为事件的神经元模型被称为 Intergrate-and-fire 模型。该模型没有尝试描述活动电位的形状。Integrade-and-fire 模型有两个独立的组成部分,都是定义其动力学所必须的:
- 描述膜电位 $u_i(t)$ 变化的方程;
- 产生脉冲的机制。
在下文中将介绍最简单的 Intergrade-and-fire 类模型:Leaky Integrade-and-fire 模型,该模型有两个独立的组成部分:
- 描述膜电位变化的线性微分方程;
- 脉冲发射的阈值。
# 1. 输入的整合(input integration)
变量 $u_i$ 描述了神经元 $i$ 的膜电位的瞬时值。在没有任何输入的情况下,电位处于静息值 $u_{rest}$ 。如果实验者向神经元 $i$ 注入电流 $I(t)$ ,或神经元 $i$ 接收其它神经元的突触输入,电位 $u_i$ 将被偏离其静止值。
为了得到一个将瞬时电压 $u_i(t) - u_{rest}$ 与输入电流 $I(t)$ 联系起来的方程,我们使用电学理论中的基本定律。一个神经元被细胞膜所包围,这是一个相当好的绝缘体。如果一个短的电流脉冲 $I(t)$ 被注入到神经元中,额外的电荷 $q=\int I(t’)\ dt’$ 必须去到某个地方:给细胞膜充电(如下图所示)。因此,细胞膜的作用就相当于一个容量为 $C$ 的电容器。因为绝缘体并不完美,电荷会随着时间的推移慢慢通过细胞膜泄露。因此,细胞膜可以用一个有限的泄露电阻 $R$ 表示。
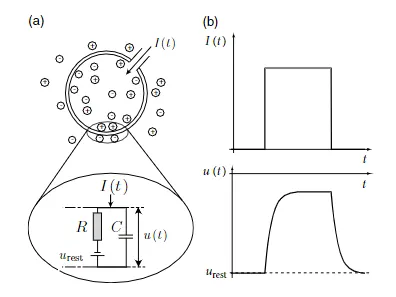
图 3.1:神经元的电学特性:被动膜。(a)由细胞膜(大圈)包围的神经元接收一个(正)输入电流 $I(t)$ ,增加细胞内的电荷。细胞膜的作用就像一个与电阻并联的电容器,与电位为 $u_{rest}$ 的电池并联。(b)细胞膜对具有平滑电压轨迹的阶梯电流的反应。
代表 Leaky Integrate-and-fire 模型的基本电路由一个电容 $C$ 和一个由电流 $I(t)$ 驱动的电阻 $R$ 并联组成。如果驱动电流 $I(t)$ 为零,则电容器两端的电压由电池电压 $u_{rest}$ 给出。
为了分析电路,我们使用电流守恒定律,将驱动电流分成两部分。
$$ I(t) = I_{R} + I_{C}. \tag{3.1} $$
第一个是通过线性电阻 $R$ 的阻性电流 $I_R$ ,根据欧姆定律可以计算出 $I_R=\frac{u_R}{R}$,其中 $u_R=u-u_{rest}$ 是电阻两端的电压。第二个分量 $I_C$ 给电容器 $C$ 充电。根据电容的定义 $C=\frac{q}{u}$ ,其中 $q$ 为电荷,$u$ 为电压,我们可以得出电容电流 $I_C=\frac{dq}{dt}=C \frac{du}{dt}$ ,即:
$$ I(t)=\frac{u(t)-u_{rest}}{R}+C \frac{du}{dt}. \tag{3.2} $$
等式两边乘以 $R$ ,并引入时间常数 $\tau_{m}=RC$ , 则标准形式为:
$$ \tau_m \frac{du}{dt} = -[u(t)-u_{rest}]+RI(t). \tag{3.3} $$
其中,$u$ 是膜电位,$\tau_m$ 是神经元的膜时间常数。
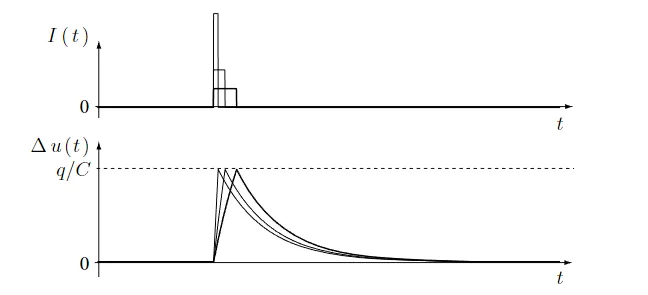
图 3.2:被动膜上的短脉冲和总充电量。由短电流脉冲 $I(t)$ 驱动的漏电整合器的电压响应振幅(底部)(顶部)只取决于总电荷 $q = \int I(t) \\ dt$ ,而不取决于电流脉冲的高度。
从数学的角度来看,公式 (3.3) 是一个线性微分方程。从电气工程师的角度来看,它是一个漏电整合器或 $RC$ 电路的方程,其中电阻 $R$ 和电容 $C$ 是平行排列的。从神经科学家的角度来看,它被称为被动膜的方程。
方程 (3.3) 的解是什么?我们假设,无论出于什么原因,在时刻 $t=0$ 时,膜电位的值为 $u_{rest} + \Delta u$ 。在 $t>0$ 时,输入电流 $I(t)$ 将消失变为零。直观地讲,我们期望,如果我们等待足够长的时间,膜电位会放松到静息电位 $u_{rest}$ 。事实上,具有初始条件 $u(t_0)=u_{rest} + \Delta u$ 的方程 (3.3) 的解是:
$$ u(t)-u_{rest}=\Delta u \exp \left ( -\frac{t-t_0}{\tau_m} \right)\ \mathrm{for}\ t>0. \tag{3.4} $$
因此,在没有输入的情况下,膜电位以指数形式衰减静息电位。膜时间常数 $\tau_m=RC$ 是衰减的特征时间。对于一个典型的神经元来说,它在 $10ms$ 的范围内,因此与 $1ms$ 数量级的脉冲持续时间相比相当长。解 (3.4) 的有效性可以通过在方程两边取导数来检查。由于它是没有输入时的解,它又被称为自由解(free solution)。
# 2. 脉冲输入(pulse input)
在我们继续定义 Intergrate-and-Fire 模型及其变体之前,让我们研究一下由公式 (3.3) 定义的被动膜的动力学。假设被动膜受到恒定输入电流 $I(t)=I_0$ 的刺激。该电流从 $t=0$ 开始,持续到 $t=Delta$ 。为了简单起见,我们假设 $t=0$ 时,膜电位为 $u_{rest}$ 。
第一步,我们计算一下膜电位的时间过程。膜电位的轨迹可以通过整合方程 (3.3) 和初始条件 $u(t_0)=u_{rest}$ 得到,即 $0 < t < \Delta$ 时的解为:
$$ u(t) = u_{rest} + RI_0 \left [ 1 - \exp \left ( -\frac{t}{\tau_m} \right ) \right ]. \tag{3.5} $$
如果输入电流从未停止,膜电位 (3.5) 将在 $t\rightarrow \infty$ 时接近渐进值 $u(\infty)=u_{rest}+RI_0$ 。一旦达到稳定状态,电容器上的电荷就不再变化。然后,所有的输入电流必须流经电阻。因此,电阻处的稳态电压是 $RI_0$ ,所哟膜的总电压是 $u_{rest}+RI_0$ 。
# 3. 脉冲发射阈值(spike firing threshold)
发射时间指的是一个给定的神经元发射动作电位 $t^f$ 的时刻。Leaky Integrate-and-Fire(LIF) 模型中的发射时间 $t^f$ 是由一个阈值标准定义的:
$$ t^f\ : \quad u(t^f) = \vartheta. \tag{3.6} $$
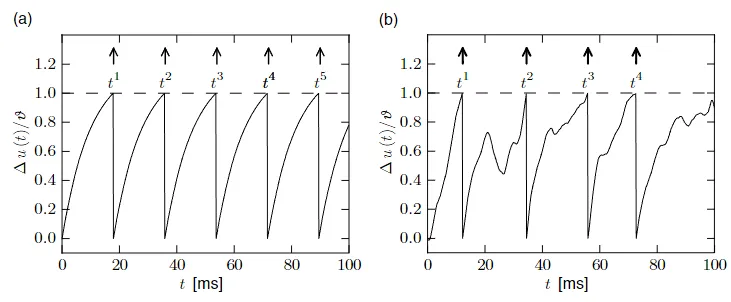
图 3.3:Integrate-and-Fire 模型。(a)由恒定输入电流 $I_0=1.5$ 驱动的 Integrate-and-fire 神经元的膜电位的事件过程。电压 $\Delta u(t)=u-u_{rest}$ 被阈值 $\vartheta$ 归一化。输入电流的单位将被选择,以便 $I_0=1$ 能对应达到 $t\rightarrow \infty$ 的阈值曲线。在一个脉冲过后,电位被重置为 $u_{\tau} = u_{rest}$ 。(b)对随时间变化的输入电流的电压反应。
虽然脉冲的形式没有被明确描述。然而注意到,在发射时间 $t^f$ 之后,电位立即被重置为一个新的值 $u_r < \vartheta$。
$$ \lim_{\delta \rightarrow 0; \delta > 0} u(t^f + \delta) = u_r. \tag{3.7} $$
对于 $t>t^f$,动力学再次由 (3.3) 给出,直到发生下一个阈值跨越。联立 (3.3) 和 (3.7),我们可以定义 Leak Integrate-and-Fire(LIF) 模型(Stein, 1967)。图 3.3 显示了由恒定电流 $I_0$ 驱动的 LIF 模型的电压曲线。
对于神经元 $i$ 的发射时间,我们定义 $t_i^f$ ,其中 $f=1,2,\cdots $ 是脉冲的标签。从形式上看,我们可以将神经元的脉冲序列表示为发射时间的序列:
$$ S_i(t) = \sum_{f} \delta (t-t_i^f). \tag{3.8} $$
其中,$\delta(x)$ 是 Dirac $\delta$ 函数:
$$ \delta(x)=\begin{cases} 0,&x = 0 \\ \int_{-\infty}^{\infty} \delta(x) dx = 1,& x \neq 0 \end{cases} \tag{3.9} $$
# 四、LIF 模型的局限性
LIF 模型是高度简化的,忽略了神经元动力学的许多细节。尤其是,可能来自突触前神经元或者电流注入的输入被线性整合,与突触后神经元的状态无关:
$$ \tau_m \frac{du}{dt} = -[u(t)-u_{rest}]+RI(t). \tag{4.1} $$
其中,$I(t)$ 是输入电流。此外,在每个输出脉冲之后,膜电位被重置。
$$ \mathrm{if}\ u(t)=\vartheta \quad\mathrm{then} \ \lim_{\delta \rightarrow 0; \delta > 0} u(t+\delta) = u_r. \tag{4.2} $$
这样就不会保留对以前脉冲的记忆。现在,让我们列出到目前位置讨论的简化模型的主要局限性。
# 1. 适应、爆发和抑制性反弹(adaptation, bursting and inhibitory rebound)
通过细胞内电极注入电流。在一个标准的实验方案中,我们可以施加一个刺激电流,在时间 $t_0$ 从一个电流值 $I_1$ 切换到一个新的电流值 $I_2$ 。假设 $I_1=0$ ,这样神经元在 $t<t_0$ 时是静息状态的。如果电流 $I_2$ 足够大,它将引起 $t>t_0$ 的脉冲。大多数神经元会对当前阶跃做出反应,产生一列脉冲,脉冲之间的间隔会连续增加,直到达到周期性发射的稳定状态。
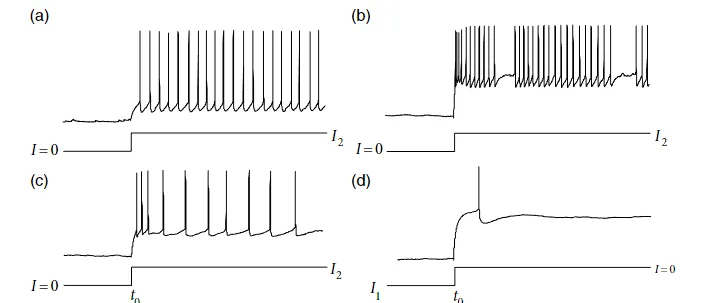
图 4.1:对当前阶跃的反应。在(a)(c)中,电流在 $t=t_0$ 时从 $I_1=0$ 切换到 $I_2>0$ 。fast-spiking neuron(a)在没有适应的情况下具有较短的脉冲间隔,而 regularly firing neuron(c)表现出适应性,可以看到脉冲间隔时间的增加。(b)中显示了一个 stuttering neuron(指发生语言或运动障碍的神经元,这种神经元在传递信号时可能会出现中断、重复或不协调的行为,导致口吃或肌肉抽动等症状)的例子。许多神经元在抑制性电流 $I_1 <0$ 被关闭后发出一个抑制性反弹脉冲(d)。
图 4.1(c)中这种具有适应性的神经元被称为 regularly firing neuron。适应是一个缓慢的过程,在几个脉冲上积累起来。由于标准的 LIF 模型在每次脉冲后将电位重置位相同的值并重新启动整合过程,因此在最近的脉冲之后不会保留任何记忆。因此,LIF 神经元不具有适应性。
第二类神经元为 fast-spiking neuron。这些神经元不显示适应性,因此可以用 LIF 模型来近似。许多抑制性神经元是 fast-spiking neuron。
除了 regularly firing neuron 和 fast-spiking neuron 外,还有 bursting neuron 和 stuttering neuron。这些神经元对恒定刺激的反应是一连串的脉冲,这些脉冲周期性地爆发或非周期性地被相当长的间隔打断。
另一个经常观察到的行为是抑制后的反弹。考虑到一个 $I_1<0$ 和 $I_2=0$ 的阶梯电流,即:在一个时间 $t_0$ 从一个抑制性电流 $I_1$ 切换到零电流。在这种情况下,许多神经元会在 $t>t_0$ 时发出一个或多个抑制性反弹脉冲,甚至抑制的释放也能出发动作电位。这种行为在图 4.1(d) 中显示。
# 2. 分流抑制和反转电位(shunting inhibition and reversal potential)
在显示中,神经元被嵌入在一个大型网络中,并接受来自许多其它神经元的输入。假设一个来自突触前神经元 $j$ 的脉冲在时间 $t_j^f$ 被发送到突触后神经元 $i$ 的突触。突触后电位是脉冲到达突触后产生的,其形状和振幅不取决于突触后神经元 $i$ 的状态。这当然是一种简化,现实中的情况要复杂一些。
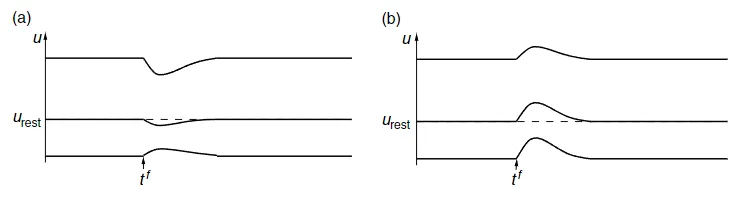
图 4.2:突触后电位的形状取决于去极化的瞬间水平。(a)当神经元处于静息状态时,在时间 $t^f$ 到达的抑制性突触的突触前脉冲对膜电位几乎没有影响,但如果膜电位 $u$ 高于静息电位,则影响很大。如果膜在抑制性突触的反转电位以下超极化,对突触前输入的反应就会改变符号。(b)兴奋性突触的脉冲引起突触后电位,其振幅仅略微取决于瞬间电压 $u$ 。对于大的去极化,振幅会饱和并且变小。
在图 4.2 中示意性地勾勒了一个实验,其中神经元由恒定电流 $I_0$ 驱动。假设 $I_0$ 太弱,无法引起发射,因此,在一定的静息时间后,膜电位会稳定在一个恒定值 $u_0$ 。在 $t=t^f$ 时,其中一个突触前神经元发出一个脉冲,这样,不久之后动作电位就会到达突触,并且提供突触后神经元的额外刺激。更精确的说,脉冲在突触后神经元产生一个电流脉冲(突触后电流,PSC),其振幅为:
$$ PSC \propto [u_0-E_{syn}] \tag{4.3} $$
其中,$u_0$ 是膜电位,$E_{syn}$ 是突触的反转电位。由于电流输入的振幅取决于 $u_0$ ,突触后电位的反应也是如此。
突触后反应对神经元瞬间状态的依赖性在抑制性突触中最为明显。抑制性突触 $E_{syn}$ 的反转电位更低,但通常接近静息电位。因此,如果神经元处于精细状态,输入脉冲对膜电位几乎没有任何影响。然而,如果膜是去极化的,同样的输入脉冲会引起更大的抑制性突触后电位;如果膜已经超极化,输入脉冲甚至可以产生去极化的效果。
虽然抑制性输入通常对膜电位只有很小的影响,但细胞膜的局部电导率可以大大增加。突触通常位于树突树的体部或轴上。由于它们的策略位置,少数抑制性输入脉冲可以“冲刷”树突树从从数百个兴奋性突触收集的整合输入。这种现象被称为分流抑制(shunting inhibition)。
兴奋性突触的反转电位通常明显高于静息电位。如果膜去极化, $u_0 \gg u_rest$ ,兴奋性突触后电位的振幅就会降低,但其效果并不像抑制那样明显。对于非常高的去极化水平,可以观察到 EPSPs 的饱和。
# 3. 脉冲后的电导率变化(conductance changes after spikes)
突触后电位的形状不仅取决于去极化的程度,而且更广泛地取决于神经元的内部状态,例如,相对于以前动作电位的时间。假设在时间 $t^f_i$ 产生了动作电位,突触前的脉冲在突触 $j$ 的时间 $t^f_j > t^f_i$ 到达。如果突触前脉冲在突触后动作电位期间或之后不久到达,它的影响不大,因为参与发射动作电位的一些离子通道依然是开放的。如果输入脉冲到达地更晚,它就会产生一个通常大小的突触后电位。
# 4. 空间结构(spatial structure)
突触后电位的形式也取决于突触在树突树上的位置。位于远离体细胞的突触引起的突触后电位通常比位于体细胞附近的突触引起的突触后电位小。如果几个输入在几毫秒内出现在同一个树突分支上,第一个输入将引起膜电位的局部变化,影响对稍晚到达的输入脉冲的反应幅度。这可能会导致饱和,或者在所谓的“活性”电流的情况下,导致反应的增强。而在 LIF 模型中,不同突触前脉冲之间这种非线性相互作用被忽略了。
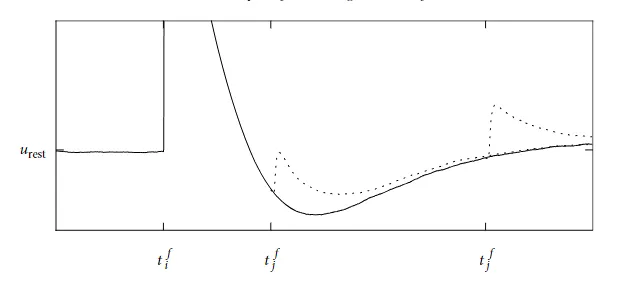
图 4.3:突触后电位的形状(虚线)取决于自神经元 $i$ 的最后一次输出脉冲以来所经过的时间 $t-t^f_i$。 突触后的尖峰在时间 $t^f_i$ 被触发。突触前的脉冲在突触后神经元的尖峰后不久到达 $t^f_j$ ,其振幅比后来到达的脉冲小得多。
# 五、LIF 模型的启示
LIF 模型是一个极其简化的神经元模型。它忽略了神经科学家在研究活脑或脑组织切片中的神经元时观察到的许多特征。因此,问题出现了:我们应该从这样一个模型中期待什么?显然,我们不能指望它能解释神经元的完整生物化学和生物物理学。我们也不期望它能解释由树突树上某些 “热点 “的活性电流引起的高度非线性的相互作用。然而,当涉及到产生脉冲时,即在时间上精确计时的事件时,LIF 模型是十分精确的。因此,它有可能成为神经元中脉冲产生的有效模型,或者更准确地说,能成为细胞体中脉冲产生的有效模型。
从脉冲生成模型中预测真实神经元脉冲的时间趋势是合理的。实验者使用第一个电极将随时间变化的输入电流 $I(t)$ 注入皮质神经元的细胞体中。通过一个独立的第二电极,实验者测量神经元体部的电压。毫不奇怪,电压轨迹不时地包含尖锐的电脉冲。这些是动作电位或脉冲。
数学神经科学家现在把实验者使用的输入电流的时间过程 $I(t)$ 与神经元膜电位的时间过程一起,调整一个 LIF 模型的参数,使该模型在输入电流相同的情况下,在时间上产生与真实神经元大致相同的脉冲。这需要一些参数调整,但似乎是可行的。然而,更难解决的相关问题是,神经元模型现在是否可以用来预测真实神经元在新的随时间变化的输入电流下的发射时间,而这种新的输入电流在参数优化过程中并未使用。
如上所述,神经元不仅在每次放电后表现出不稳定,而且还表现出在数百毫秒内积累起来的适应能力。简单的 LIF 模型并不能很好地预测真实神经元的脉冲时间。然而,如果在神经元模型中加入适应性(和不稳定因素),预测结果就会出奇地好。增加适应性的一种直接方法是使神经元模型的放电阈值动态:在每个脉冲之后,将阈值 $\vartheta$ 增加一个增量 $\theta$ ,使得静息期间,阈值接近其固定值 $θ_0$ 。我们可以使用 Dirac $\delta$ 函数来表示这种动态阈值:
$$ \tau_{adapt} \frac{d\vartheta}{dt} = -[\vartheta(t)-\vartheta_0] + \theta \sum_{f} \delta(t-t_i^f). \tag{5.1} $$
其中,$\tau_{adapt}$ 为适应时间常数(~几百毫秒),$t^f=t^{(1)}, t^{(2)}, t^{(3)}, \cdots$ 是神经元的发射时间。
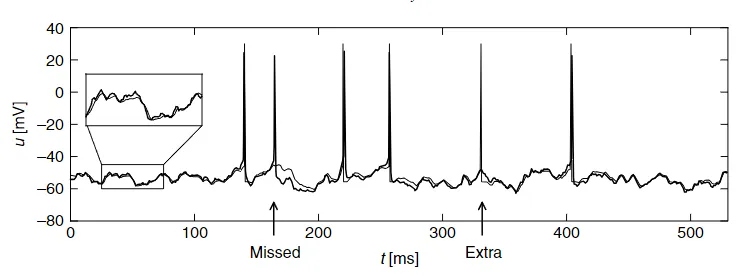
图 5.1: 广义 LIF 模型与真实实验测量的对比。由波动电流驱动的真实神经元中记录的电压曲线(粗黑线)被叠加在由相同电流驱动的广义 LIF 模型(细线)上。除了少数额外或遗漏的脉冲(箭头),平均脉冲时间也得到了很好的预测。
从图 5.1 中可以看出,具有动态阈值的 LIF 模型的预测结果与真实神经元的电压曲线非常吻合。
一旦我们确定了好的候选神经元模型,我们将可以尝试用这些模型构建大的神经元网络,并进一步尝试理解神经元网络所使用的动态和计算原理以及潜在的神经编码。虽然这并不意味着理解了整个大脑,但经过良好测试的简化神经元模型中理解大量神经元群体的原理是朝着这个方向迈出的第一步,也是重要的一步。
# 总结
神经元信号由短电压脉冲组成,称为动作电位或者脉冲。这些脉冲沿着轴突行进,并被分配到几个突触后神经元,在那里它们又引起突触后电位。如果一个突触后神经元在一个短时间窗口内从多个突触前神经元那收集到足够多的脉冲,它的膜电位可能会达到一个临界值,然后发射出一个脉冲。我们说,神经元已经“发射”了一个脉冲。这个脉冲是神经元的输出信号,反过来又被传输到其它神经元。
一个比较简单的脉冲神经元模型是 LIF 模型。该模型用一个线性微分方程描述了输入电流如何被整合并转化为膜电位 $u(t)$ 。这里的输入可以是实验者注入孤立神经元的输入电流,也可以是由大型高度连接网络中其它神经元到达的脉冲引起的突触输入电流。其次,如果膜电位到达阈值 $\vartheta$ ,LIF 神经元会产生一个输出脉冲。最后,在脉冲发射后,线性整合过程被重置,膜电位被重置为一个新的值 $u_r$ 。这个过程被称为膜电位的重置。
LIF 模型并没有考虑持久的适应性,然而,如果 LIF 模型的电压动态地通过适应机制得到增强,那么它可以成为准确预测皮层神经元脉冲时间的有力工具。
