# 最小反馈弧集合问题

# 一、引言

在复杂网络分析、社会学、生物信息学等领域，我们经常需要处理的一个问题是如何从一个有向图中移除最少的边，使得图中不再存在环。这个问题被称为最小反馈弧集问题（Minimum Feedback Arc Set，简称 MinFAS）。在本文中，我们将详细介绍这个问题的定义、性质，以及一些常见的解决算法。我们还将讨论这个问题在实际应用中的一些例子。

# 二、问题定义

首先，我们来详细定义一下最小反馈弧集问题。给定一个有向图 G=(V, E)，其中 V 是顶点集，E 是边集。给定有向图 G(V,E)，集合 F 是 E 的一个子集，若 G 的生成子图 G′(V,E−F)中不包含环，则称 F 是 G 的一个反馈弧集合。容易推出：若有向图 G 包含环，则其每个环至少有一条边在 F 中。我们将基数最小的反馈弧集合称为最小反馈弧集合。最小反馈弧集合问题就是在给定有向图 G 的情况下，求解最小反馈弧集合 F。

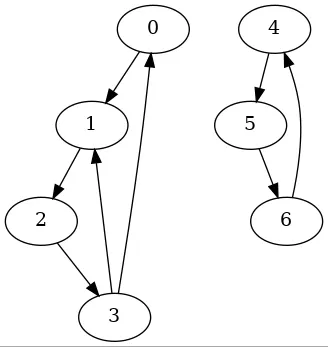
例如：$ F={(1, 2), (4, 5)} $

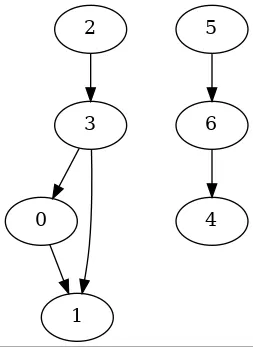
在这个问题中，我们的目标是找到最小的反馈弧集，也就是说，我们希望找到尽可能少的边，使得去掉这些边后图中不再有环。这个问题在许多实际应用中都有重要的意义。例如，在社会网络分析中，我们可以通过这个问题来找出社区内的关键人物；在生物信息学中，我们可以通过这个问题来找出基因调控网络中的关键基因。

最小反馈弧集问题已经被证明是一个 NP 难问题。这意味着，我们无法在多项式时间内找到这个问题的精确解（除非 P=NP）。然而，尽管这个问题很难，但是我们仍然可以通过一些方法来找到它的近似解。在理论计算机科学中，有一类算法被称为近似算法，它们可以在多项式时间内找到问题的近似解。对于最小反馈弧集问题，我们也可以使用这类算法来求解。在接下来的部分中，我们将介绍一些常见的近似算法。

# 三、解决方案

对于最小反馈弧集问题，我们有多种解决方案，其中包括贪心算法（GreedyFAS）、排序算法（SortFAS）和基于 PageRank 的算法（PageRankFAS）。

# 1. GreedyFAS

GreedyFAS 算法的核心思想在于用贪心法生成一个线性排列，将该线性排列中的后向边集作为结果返回。该算法的伪代码如下图所示：

对任一有向图 G，GreedyFAS 算法使用的贪心策略为：

查找源头点（入度为 0 的点）。若查到源头点则排在序列 $s_1$ 末尾并移除该点，重复直到 $G$ 无源头点。
查找汇集点（出度为 0 的点）。若查到汇集点则排在序列 $s_2$ 首部并移除该点，重复直到 $G$ 无汇集点。
计算剩余点的 $\delta$ 值（出度与入度的差值），将 $\delta$ 值最大的点排在 $s_1$ 末尾并移除该点。
重复上述过程直到 $G$ 不存在任何点。
返回序列 $s_1 s_2$ 。

# 2. SortFAS

SortFAS 算法的基本思想是该算法根据序号的自然顺序生成初始最小线性排列问题（LA），不断调整 LA 使后向边的数量尽可能少。该算法的伪代码如下图所示：

对任一有向图 G，SortFAS 算法的步骤如下：

生成初始最小线性排列问题（LA）。
对于 LA 中的每个序号 v，记录全局变量 val，初始化为 0，表示调整后新增的后向边数。记录 v 的位置 loc。记录最小值 min=0
- 从序号 loc-1 开始，向前遍历 LA 得到序号 w，若 v->w 存在则 val–，否则 val++。
- 如果 val 小于等于 min，则赋值 min=val，记录位置 loc=w
- 在位置 loc 插入序号 v

# 3. PageRankFAS

PageRankFAS 算法的核心思想在于将原始图的强连通分量转换为线图，然后用 PageRank 算法评估线图中节点的重要性，然后依次删除线图中 PageRank 值最高的节点对应的边。该算法的伪代码如下图所示：

对任一有向图 G，PageRankFAS 的算法步骤如下：

检测图是否有环，如果存在环，执行以下循环：

识别有向图中的强连接分量 $s_i, i=0,1,\cdots$
遍历强连通分量 $s_i$ ，对于每个强连通分量 $s_i$ ，执行：
- 如果 $s-i$ 的大小小于等于 1，跳过该强连通分量的处理。
- 选择 $s_i$ 中的一个随机节点 $v$ ，从 $v$ 开始遍历创建 $s_i$ 的线图 $L(s_i)$
- 计算 $L(s_i)$ 的 PageRank 值。
- 选择 $L(s_i)$ 中 PageRank 值最大的节点，找到 $s_i$ 中对应的边 $e$ ，添加到最小反馈弧集。
- 在 $G$ 中删除边 $e$ 。
如果仍有环，重复执行 1 和 2，直到图不存在环为止。

# 四、实际应用

最小反馈弧集问题在许多领域都有广泛的应用。例如，在生物信息学中，我们可以通过求解最小反馈弧集问题，来找出基因调控网络中的关键基因。在这种情况下，我们通常将基因调控网络表示为一个有向图，其中的顶点代表基因，边代表基因之间的调控关系。然后，我们可以通过求解最小反馈弧集问题，来找出那些对整个网络有重要影响的基因。

在社会网络分析中，我们可以通过求解最小反馈弧集问题，来检测社区内的关键人物。在这种情况下，我们通常将社区表示为一个有向图，其中的顶点代表人，边代表人之间的关系。然后，我们可以通过求解最小反馈弧集问题，来找出那些对整个社区有重要影响的人。